AP Pre-Calculus: Unit 3 - Trigonometric and Polar Functions Study Guide

Welcome to your ultimate guide for Unit 3! This unit dives into the fascinating world of trigonometric and polar functions. Get ready to explore how these concepts apply to real-world scenarios and boost your confidence for the AP exam. Let's make this click! 🚀

Unit 3 Overview: Trigonometric and Polar Functions

Unit 3 is all about trigonometric and polar functions, covering everything from the basics to advanced applications. This unit is crucial for understanding how math models the world around us. You'll be using these concepts to:

1. Analyze and model real-world phenomena.
2. Solve problems in mathematics and other fields.

Real-World Applications

Trigonometric and polar functions aren't just abstract math concepts; they have tons of real-world applications:

1. 🧮 Mathematics: Used in calculus, geometry, and linear algebra for finding lengths, angles, and solving equations.
2. ☢️ Physics: Used to describe motion, position, wave motion (sound and light), and oscillations.
3. 🛠 Engineering: Used to solve problems involving angles, distances, and positions in mechanical, electrical, and computer graphics fields.
4. 💻 Computer Science: Used in computer graphics for 2D/3D images and animations, and in computer vision for shape detection.
5. 🔭 Astronomy: Used to find positions of celestial bodies, calculate distances, and predict their movements.
6. 💰 Economics: Used to model and analyze market trends and consumer behavior.
7. 🧬 Biology: Used to study shapes and structures of living organisms, such as plant growth and animal movement.
8. 🌧 Meteorology: Used to study weather systems like hurricanes and tornadoes.
9. 🏛 Architecture: Used to design and construct buildings and bridges, ensuring stability and security.

Unit Breakdown

🔀 Periodic Phenomena

Periodic phenomena are patterns that repeat over time. Think of a swing or a heartbeat. 🎠

• Trigonometric functions like sine and cosine are perfect for modeling these patterns.
• You'll learn to identify and analyze these patterns and use trig functions to model them.

Sine and cosine function graphs

2️⃣ The Big Two: Sine and Cosine

• Sine and cosine values help find coordinates on a circle.
• The unit circle is your best friend for finding values at special angles.
• You'll be sketching and analyzing graphs to find period, amplitude, and vertical shift. 📈

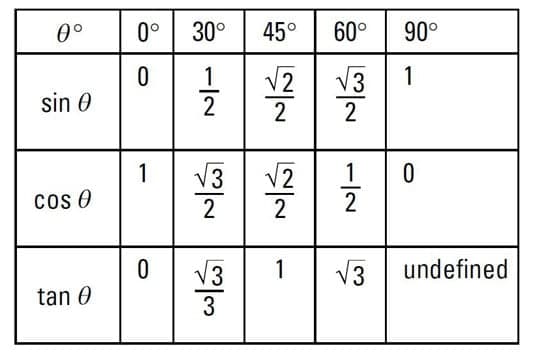
Trigonometric function values

⏺ Sinusoidal Functions and the Tangent Function

Sinusoidal functions are periodic functions represented by sine or cosine. They model things like sound and light waves. 🌊

• Transformations (shifts, stretches, compressions) change the look of sinusoidal functions. You'll use these to model real-world data.
• You'll learn how to analyze data and make predictions using these models. 🤔
• The tangent function helps find the slope of a line. ↗️

Unit Circle

⏪ Inverse Trigonometric Functions

Inverse trigonometric functions help you find the angles that match a given sine, cosine, or tangent value. 🏃

• Great for solving problems involving angles and distances.
• You’ll use these to solve trigonometric equations and inequalities. 🤓

Inverse Trigonometric Functions

3️⃣ The Other Three: Secant, Cosecant, and Cotangent

• These are the reciprocals of sine, cosine, and tangent, respectively.
• You'll learn how to use them and relate them to the main trig functions.
• Equivalent representations help express trig functions in different forms. 🧐

Trigonometric Identities

🌀 Polar Coordinates and Functions

Polar coordinates are another way to express positions in a plane. ✈️

• You'll learn to use polar coordinates and trigonometry to find distances and angles between points.
• Polar function graphs help represent functions in polar coordinates. You'll learn how to sketch and analyze them. 💫
• Rates of change in polar functions describe how a function’s value changes with respect to the angle.

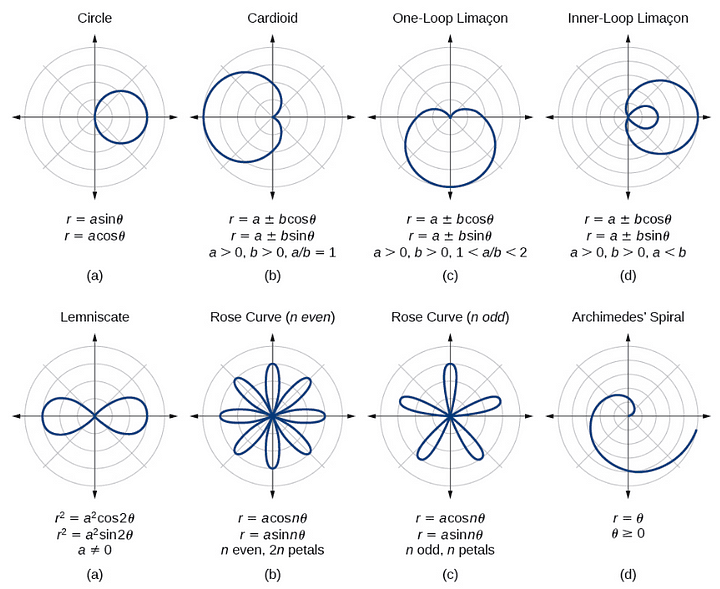
Polar function graphs

Pay special attention to transformations of sinusoidal functions and polar coordinates. These are high-value topics on the AP exam. 💯

Final Exam Focus

Okay, deep breath! Here's what to focus on for the exam:

• High-Priority Topics:
  • Sinusoidal Functions: Transformations, modeling, and analysis.
  • Unit Circle: Mastering values for special angles.
  • Polar Coordinates: Graphing and understanding rates of change.
  • Inverse Trig Functions: Solving equations and inequalities.
• Common Question Types:
  • Graphing and analyzing trigonometric functions.
  • Modeling real-world scenarios with sinusoidal functions.
  • Solving trigonometric equations and inequalities.
  • Working with polar coordinates and functions.
• Last-Minute Tips:
  • Time Management: Don't get stuck on one question. Move on and come back if time permits.
  • Common Pitfalls: Double-check your unit circle values and pay attention to the domain and range of inverse trig functions.
  • Challenging Questions: Break down complex problems into smaller, manageable steps. Draw diagrams if needed.

Practice Questions

Here are some practice questions to get you warmed up:

Practice Question

Multiple Choice Questions

1. What is the amplitude of the function $f(x) = -3 \cos(2x) + 1$? (A) -3 (B) 3 (C) 2 (D) 1

2. Which of the following is equivalent to $\sin(x)$? (A) $\cos(x - \frac{\pi}{2})$ (B) $\cos(x + \frac{\pi}{2})$ (C) $\cos(x)$ (D) $-\cos(x)$

3. A point in polar coordinates is given by $(2, \frac{5\pi}{6})$. What are the rectangular coordinates of this point? (A) $(\sqrt{3}, -1)$ (B) $(-\sqrt{3}, 1)$ (C) $(1, -\sqrt{3})$ (D) $(-1, \sqrt{3})$

Free Response Question

A Ferris wheel with a radius of 25 meters completes one rotation every 2 minutes. The bottom of the wheel is 2 meters above the ground. A rider starts at the bottom of the wheel.

(a) Write a sinusoidal function that models the rider's height above the ground, h, in meters as a function of time, t, in minutes. [3 points]

(b) How high above the ground is the rider after 30 seconds? [2 points]

(c) At what time(s) during the first 4 minutes is the rider 30 meters above the ground? [4 points]

Scoring Breakdown:

(a) [3 points]

• 1 point for correct amplitude (25)
• 1 point for correct vertical shift (27)
• 1 point for correct period and phase ($\pi t$)

(b) [2 points]

• 1 point for correct substitution of t = 0.5 minutes
• 1 point for correct calculation (27 - 25cos(0.5$\pi$) = 27)

(c) [4 points]

• 1 point for setting up the correct equation: 30 = 27 - 25cos($\pi t$)
• 1 point for isolating the cosine term: cos($\pi t$) = -3/25
• 1 point for finding the first solution: t ≈ 0.54
• 1 point for finding the second solution: t ≈ 1.46

You've got this! Remember to review your notes, practice problems, and stay confident. You're well-prepared to ace this exam! 💪