Limits and Continuity
Benjamin Wright
10 min read
Listen to this study note
Study Guide Overview
This study guide covers limits and continuity in AP Calculus AB/BC. Key topics include: average and instantaneous rates of change, defining and estimating limits (from graphs and tables), algebraic properties and manipulations of limits, the Squeeze Theorem, types of discontinuities, defining continuity at a point and over an interval, removing discontinuities, asymptotes, and the Intermediate Value Theorem (IVT).
#AP Calculus AB/BC: Limits and Continuity - Your Night-Before Guide 🚀
Hey there, future calculus conqueror! This guide is your go-to resource for a final review of limits and continuity. Let's make sure you're feeling confident and ready to ace that exam! Remember, this unit is about 10-12% of the AP Calculus AB exam and 4-7% of the AP Calculus BC exam, so let's get it down!
#Introduction to Calculus
#The Big Question: Can Change Happen Instantly?
Calculus is all about change and motion. We're diving into whether change can occur at a single moment. Think of an arrow moving across a screen. It seems to jump from one spot to the next, but is it truly instantaneous? This leads us to the concept of the limit.
#1.1 Introducing Calculus: Average vs. Instantaneous Rate of Change
- Average Rate of Change (AROC): The slope of the secant line between two points on a function. It's like finding the average speed over a time interval.
- Formula:
- Instantaneous Rate of Change (IROC): The slope of the tangent line at a single point on a function. It's like finding the speed at a specific moment. We'll get to this using limits!
- Formula:

#Image courtesy of Medium.
- AROC is undefined when the denominator is zero (division by zero is a big no-no!).
#1.2 Defining Limits and Using Limit Notation
#What is a Limit?
A limit is the value a function approaches as the input (x-value) gets closer to a certain point. It helps us understand what happens at a specific point, even if the function isn't defined there. 💡

#Limit Notation
- Read this as: "The limit of f(x) as x approaches 'a' is L."
- Think of it like this: As x gets super close to 'a', the function f(x) gets super close to L.

#1.3 Estimating Limits from Graphs
#One-Sided vs. Two-Sided Limits
-
One-Sided Limit: The limit as x approaches a value from either the left or the right.
-
Two-Sided Limit: The limit as x approaches a value from both the left and the right. For a two-sided limit to exist, both one-sided limits must be equal.
- If the function approaches the same y-value from both sides, the limit exists. If not, the limit does not exist (DNE).
- Watch out for oscillations, unbounded behavior, and vertical asymptotes – these can cause limits to DNE.
#1.4 Estimating Limits from Tables
#Approaching from Both Sides
- Look at the function's values as x gets closer to the target value from both the left and the right.
- If the function approaches the same value from both sides, the limit exists. If not, the limit does not exist.

| x | 1.9 | 1.99 | 1.999 | 2 | 2.001 | 2.01 | 2.1 |
|---|---|---|---|---|---|---|---|
| f(x) | -10 | -100 | -1000 | ? | 1000 | 100 | 10 |
- Don't assume a limit exists just because the function is defined at a point. Always check both sides!
#1.5 Using Algebraic Properties of Limits
#Limit Laws
These properties help us break down complex limits into simpler ones. They’re pretty intuitive, but it’s good to be familiar with them.

#1.6 Using Algebraic Manipulations
#Four Key Techniques
-
Substitution: Plug in the value. If it works, you're done! (But be careful of division by zero!)
-
Factoring: Factor the numerator and/or denominator to cancel out common factors.
-
Common Denominator: Combine fractions by finding a common denominator.
-
Conjugate Multiplication: Multiply by the conjugate to eliminate square roots in the numerator or denominator.
- Remember SFCC: Substitute, Factor, Common Denominator, Conjugate.
#1.8 Squeeze Theorem (Sandwich Theorem)
#The Pinching Principle
If a function is "sandwiched" between two other functions that approach the same limit, then the function in the middle also approaches that limit.

#1.10 Exploring Types of Discontinuities
#Discontinuity Types
- Jump Discontinuity: The function "jumps" from one value to another.
- Removable Discontinuity: A "hole" in the graph that can be "filled" by redefining the function.
- Infinite Discontinuity: A vertical asymptote where the function approaches infinity or negative infinity.
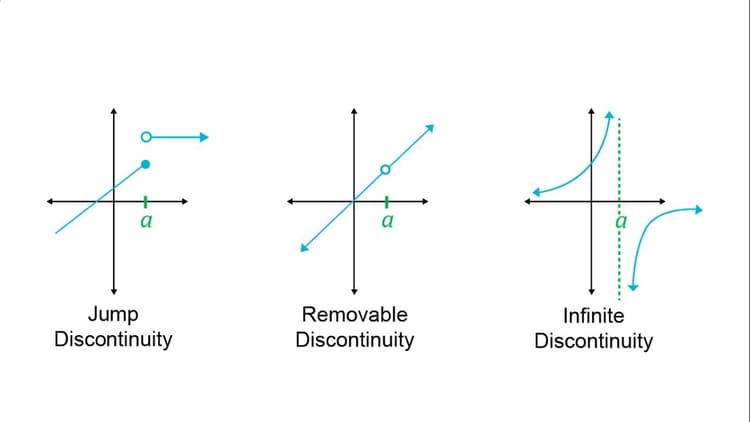
#Image courtesy of Matlab and Maths Tutorials.
#1.11 Defining Continuity at a Point
#The Three Requirements for Continuity
For a function to be continuous at a point x=a, three conditions must be met:
-
f(a) is defined (there's a y-value at x=a).
-
The limit of f(x) as x approaches a exists.
-
The limit of f(x) as x approaches a is equal to f(a).
- Think of it as: The function exists, the limit exists, and they match! 🤝

#1.12 Confirming Continuity Over an Interval
#Continuity Over an Interval
A function is continuous over an interval if it meets the three continuity conditions at every point in that interval.
#Common Continuous Functions
-
Polynomials: Always continuous everywhere.
-
Rational Functions: Continuous everywhere except where the denominator is zero.
-
Trigonometric Functions: Continuous over their domains.
-
Exponential Functions: Continuous everywhere.
- Absolute value functions and 1/x are not continuous at x=0.
#1.13 Removing Discontinuities
#Redefining the Function
If a limit exists at a point of discontinuity, you can redefine the function at that point to make it continuous. This usually involves creating a piecewise function.
#1.14 & 1.15 Asymptotes
#Vertical Asymptotes
- Found where the denominator of a rational function equals zero.
#Horizontal Asymptotes
- Compare the degrees of the numerator and denominator:
- Degrees are equal: Horizontal asymptote at the ratio of leading coefficients.
- Numerator degree is larger: Slant asymptote.
- Denominator degree is larger: Horizontal asymptote at y = 0. ## 1.16 Working with the Intermediate Value Theorem (IVT)
#The IVT Explained
If a function is continuous on a closed interval [a, b], it must take on every value between f(a) and f(b) at least once within that interval. It's like a continuous path that can't skip any values!
- Think of it as: If you draw a continuous line from point A to point B, you have to cross every y-value between A and B.

#Image courtesy of Quizlet.
- Make sure the function is continuous before applying IVT!
#Final Exam Focus
#High-Priority Topics
- Limits: Evaluating limits graphically, numerically, and algebraically. Special attention to limits involving infinity.
- Continuity: Understanding the three conditions for continuity at a point and over an interval. Identifying and classifying discontinuities.
- IVT: Applying the Intermediate Value Theorem to prove the existence of solutions.
#Common Question Types
- Multiple Choice: Evaluating limits, identifying discontinuities, applying IVT.
- Free Response: Proving continuity, finding asymptotes, using the squeeze theorem, applying IVT in context.
#Last-Minute Tips
- Time Management: Don't spend too long on one question. Move on and come back if you have time.
- Common Pitfalls: Double-check for division by zero, remember to check one-sided limits, and ensure continuity before applying IVT.
- Strategies: Show all work, even if you think it's obvious. Partial credit is your friend!
#Practice Questions
Practice Question
#Multiple Choice
-
What is the value of ? (A) 0 (B) 3 (C) 6 (D) Does not exist
-
For what value of k is the following function continuous at x = 2?
(A) -1 (B) 0 (C) 1 (D) 2
-
Given the function , which of the following statements is true? (A) f(x) has a removable discontinuity at x=2 (B) f(x) has a jump discontinuity at x=2 (C) f(x) has an infinite discontinuity at x=2 (D) f(x) is continuous for all real numbers
#Free Response Question
Consider the function:
(a) Find . (b) Find . (c) Is f(x) continuous at x = 2? Justify your answer. (d) If f(x) is discontinuous at x=2, what type of discontinuity is it?
#Scoring Rubric:
(a) 2 points
- 1 point for factoring the expression
- 1 point for correct limit value
(b) 2 points
- 1 point for correct substitution
- 1 point for correct limit value
(c) 3 points
- 1 point for stating that the function is discontinuous
- 1 point for referencing that the limit does not equal the function value at x=2
- 1 point for correct justification
(d) 1 point
- 1 point for correctly identifying the type of discontinuity
#Solutions:
Multiple Choice
- (C) 6
- (C) 1
- (C) f(x) has an infinite discontinuity at x=2
Free Response (a) (b) (c) No, f(x) is not continuous at x=2 because which does not equal (d) f(x) has a removable discontinuity at x=2
You've got this! Go get that 5! 💪
Continue your learning journey

How are we doing?
Give us your feedback and let us know how we can improve





