Using the Mean Value Theorem

#5.1 Using the Mean Value Theorem

In the previous unit, we learned all about applying derivatives to different real-world contexts. What else are derivatives useful for? Turns out, we can also use derivatives to determine and analyze the behaviors of functions! 👀

#📈  Mean Value Theorem

The Mean Value Theorem states that if a function f is continuous over the interval $[a, b]$ and differentiable over the interval $(a, b)$, then there exists a point $c$ within that open interval $(a,b)$ where the instantaneous rate of change of the function at $c$ equals the average rate of change of the function over the interval $(a, b)$.

In other words, if a function f is continuous over the interval $[a, b]$ and differentiable over the interval $(a, b)$, there exists some $c$ on $(a,b)$ such that $f'(c)=\frac{f(b)-f(a)}{b-a}$.

!Untitled

Visual representation of mean value theorem

Image Courtesy of Sumi Vora and Ethan Bilderbeek

Yet another way to phrase this theorem is that if the stated conditions of continuity and differentiability are satisfied, there is a point where the slope of the tangent line is equivalent to the slope of the secant line between $a$ and $b$.

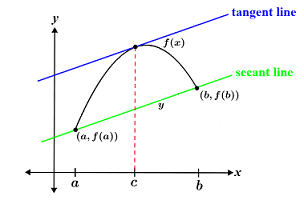
Graph depicting the Mean Value Theorem

Image Courtesy of Math.net

Remember from Unit 1, to be continuous over $[a, b]$ means that there are no holes, asymptotes, or jump discontinuities between points a and b. Because the interval contains closed brackets, the graph must also be continuous at points $a$ and $b$.

Additionally, if we recall from previous guides, to be differentiable over $(a, b)$ means that the function is continuous over the interval and that for any point $c$ over the interval, $\lim_{x\to c} \frac{f(x) - f(c)}{x - c}$ exists.

#✏️ Mean Value Theorem: Walkthrough

We can use the Mean Value Theorem to justify conclusions about functions by applying it over an interval. For example:

Let $f$ be a differentiable function. The table gives its selected values:

Can we use the Mean Value Theorem to say the equation $f'(x)=5$ has a solution where $3< x<9$?

Since it is given that $f$ is differentiable, we can apply the Mean Value Theorem (MVT) on the interval $(3,9)$. This is what we should write out!

Since $f$ is continuous and differentiable on $(3,9)$, MVT can be applied. The MVT states that there exists a $c$ on $(3,9)$ such that $f'(c)=\frac{f(9)-f(3)}{9-3}=\frac{44-20}{9-3}=\frac{24}{6}=4.$

$4 \neq 5$ so MVT cannot be used to say that $f'(x)=5$ has a solution.

---

#📝 Mean Value Theorem: Practice Problems

Now, it’s time for you to do some practice on your own! 🍀

#❓ Mean Value Theorem: Practice

#Question 1: Mean Value Theorem

Let $h(x)=x^3+3x^2$ and let $c$ be the number that satisfies the Mean Value Theorem for $h$ on the interval $[-3,0]$.

What is $c?$

#Question 2: Mean Value Theorem

Let $f$ be a differentiable function. The table gives its selected values:

Can we use the Mean Value Theorem to say the equation $f'(x)=2$ has a solution where $2<x<9$?

#✅ Mean Value Theorem: Answers and Solutions

#Question 1: Mean Value Theorem

Since $h$ is a polynomial, $h$ is continuous on $[-3,0]$ and differentiable on $(-3,0)$. Therefore, the Mean Value Theorem can be applied. By the Mean Value Theorem, there exists a $c$ on $(-3,0)$ such that…

$$f'(c)=\frac{f(0)-f(-3)}{0-(-3)}=\frac{0-0}{3}=0.$$

To find $c$, we need to differentiate $f(x)$ and find $c$ such that $f'(c)=0.$

$$f'(x)=3x^2+6x$$

$$3x^2+6x=0$$

By the quadratic formula, we have $x=-2,0$.

Since only $x=-2$ is in the interval $(-3,0)$, $c=-2.$ Great work! Make sure you remember to check if the value(s) you get are in the given interval.

#Question 2: Mean Value Theorem

Since it is given that $f$ is differentiable, we can apply the Mean Value Theorem (MVT) on the interval $(2,9)$.

The MVT states that there exists a $c$ on $(2,9)$ such that $f'(c)=\frac{f(9)-f(2)}{9-2}=\frac{35-14}{9-2}=\frac{21}{7}=3.$ $3 \neq 2$ so MVT cannot be used to say that $f'(x)=2$ has a solution.

---

#💫 Closing

The Mean Value Theorem states that for any continuous function on a closed interval, there exists a value c in the interval such that the value of the derivative of the function at c is equal to the average rate of change of the function over the interval. By using this theorem, we can find the mean value of a function on a given interval, which can provide useful information about the behavior of the function. 🧐