Periodic Waves
Owen Perez
8 min read
Listen to this study note
Study Guide Overview
This study guide covers periodic waves, including their key characteristics (period, frequency, wavelength, speed, amplitude, and waveform). It explains transverse and longitudinal wave types, the relationship between period and frequency, and how to describe waves as functions of time and position using sine/cosine equations. The guide also covers the general wave equation, interpreting wave graphs, and practice problems involving wave properties and calculations. Finally, it provides exam tips and strategies for success.
#Periodic Waves: Your Ultimate Guide 🌊
Hey there, future AP Physics 2 master! Let's dive into the world of periodic waves. Don't worry, it's not as intimidating as it sounds. Think of it as a fun, repeating dance!
#What is a Periodic Wave?
A periodic wave is simply a wave that repeats its pattern over and over again. It's like a never-ending rollercoaster ride, with each hill and valley looking the same. These waves are characterized by their wavelength, period, frequency, and amplitude.
#Key Characteristics:
-
Period (T): The time it takes for one complete wave cycle. Think of it as the duration of one 'wave dance'.
-
Frequency (f): How many wave cycles happen in one second, measured in Hertz (Hz). It's like the tempo of the wave dance.
-
Wavelength (λ): The distance between two identical points on a wave (e.g., crest to crest). Imagine measuring the length of one 'wave dance' on the floor.
-
Speed (v): How fast the wave is traveling, calculated as v = fλ.
-
Amplitude (A): The maximum displacement of the wave from its resting position. It's the height of the 'wave dance' from the middle.
-
Waveform: The shape of the wave (e.g., sine, cosine).
-
Types: Periodic waves can be transverse (displacement perpendicular to wave direction, like a guitar string) or longitudinal (displacement parallel to wave direction, like a slinky).
Understanding the relationship between period and frequency is crucial: and .
#The Wave Equation
In AP Physics 2, we often use sine or cosine functions to describe simple periodic waves. These equations help us understand how the wave changes with time and position.
#Wave as a Function of Time:
- where
- where
#Wave as a Function of Position:
Where:
- A = Amplitude
- T = Period
- f = Frequency
- λ = Wavelength
- t = Time
- x = Position
- ω = Angular Frequency
Pay close attention to whether the wave is described as a function of time or position. The equations are slightly different!
#Example: Reading a Wave Graph
Let's decode a wave graph together.
- General Equation (Position):
- Amplitude (A): The highest point on the graph is 4, so A = 4. 3. Wavelength (λ): The distance between crests is 6 - 3 = 3, so λ = 3. Therefore, the equation for this wave is:
#The General Wave Equation
The general wave equation is a partial differential equation that describes the relationship between the displacement of a wave and the time and space variables that define the wave:
Where:
- y is the displacement of the wave
- t is time
- x is space
- c is the speed of the wave
Don't confuse the general wave equation (a partial differential equation) with the specific equations for periodic waves (using sine or cosine).
#Practice Problems 🧩
Time to test your knowledge! Let's tackle some practice problems to solidify your understanding.
-
The frequency of the tuning fork is (approximately)...
A) 0.0039 s B) 0.020 s C) 2.55 Hz D) 50 Hz E) 256 Hz
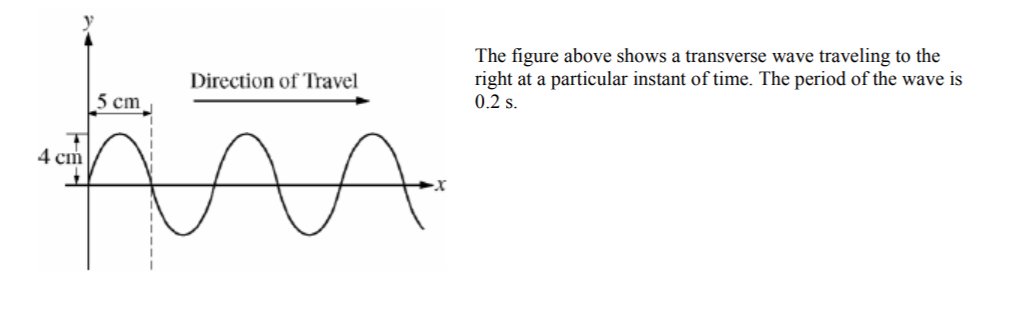 -
What is the amplitude of the wave?
(A) 4 cm (B) 5 cm (C) 8 cm (D) 10 cm (E) 16 cm
-
What is the speed of the wave?
(A) 4 cm/s (B) 25 cm/s (C) 50 cm/s (D) 100 cm/s (E) 200 cm/s
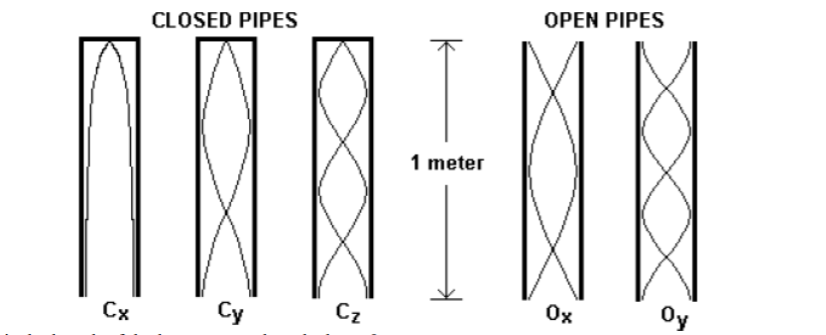 -
What is the length of the longest wavelength shown?
A) 0.5 m B) 0.75 m C) 1 m D) 2 m E) 4 m
-
Which organ pipe(s) shows a standing wave which has twice the frequency of one of the other waves shown?
A) Cy B) Cz C) Ox D) Oy E) Cy , Cz, Ox, Oy
#Answers
- E: f = cycles / seconds
- A: By inspection
- C: By inspection, the λ is 10 cm. f = 1 / T = 5, Then use v = f λ.
- E: Cx is only ¼ of a wavelength. To make a full wavelength you would need 4x the current length
- D: Wavelengths of each are (dist/cycle) … 4L, 4/3 L, 4/5 L, L, 2/3 L …Frequencies are f = v/ λ.v/4L, 3v/4L, 5v/4L, v/L, 3v/2L … Oy is 2x Cy
Practice Question
#Multiple Choice Questions:
-
A wave has a frequency of 10 Hz and a wavelength of 2 meters. What is the speed of the wave? (A) 5 m/s (B) 12 m/s (C) 20 m/s (D) 0.2 m/s
-
If the amplitude of a wave is doubled, what happens to its energy? (A) It doubles (B) It quadruples (C) It halves (D) It remains the same
#Free Response Question:
A transverse wave on a string is described by the equation , where x and y are in meters and t is in seconds.
(a) What is the amplitude of the wave? (b) What is the wavelength of the wave? (c) What is the frequency of the wave? (d) What is the speed of the wave?
#Scoring Rubric for FRQ:
(a) 1 point: Amplitude = 0.2 m (correctly identified from the equation) (b) 2 points: * 1 point for recognizing that corresponds to * 1 point for calculating the wavelength: m (c) 2 points: * 1 point for recognizing that corresponds to * 1 point for calculating the frequency: f = 2 Hz (d) 2 points: * 1 point for using the formula v = fλ * 1 point for calculating the speed: v = 2 m/s
#Final Exam Focus 🎯
Alright, you've come a long way! Here's what to focus on for the final exam:
- High-Value Topics: Wave characteristics (wavelength, frequency, amplitude, speed), wave equations (both time and position), and the relationship between them.
- Common Question Types: Calculating wave speed, identifying wave properties from graphs, and applying the wave equation to solve problems.
- Time Management: Quickly identify key information in the problem and apply the correct formulas. Don't get bogged down in complex calculations; focus on the core concepts.
- Common Pitfalls: Mixing up time and position equations, misinterpreting wave graphs, and forgetting the relationship between period and frequency.
- Strategies: Practice, practice, practice! Work through as many problems as possible, and make sure you understand the underlying concepts, not just the formulas.
Remember "V=fλ" (Velocity equals frequency times wavelength) - it's your best friend for wave calculations!
The speed of a wave depends on the medium it travels through, not its frequency or wavelength.
Always double-check your units! Make sure everything is consistent (e.g., meters, seconds, Hertz).
You've got this! Stay calm, trust your preparation, and remember that physics is all about understanding the world around you. Good luck on your exam! 🎉
Continue your learning journey

How are we doing?
Give us your feedback and let us know how we can improve





