Inverse Trigonometric Functions
Henry Lee
7 min read
Listen to this study note
Study Guide Overview
This study guide covers inverse trigonometric functions for AP Pre-Calculus. It reviews basic trigonometric functions (sine, cosine, tangent) and their inverses (arcsine, arccosine, arctangent). It emphasizes domain and range restrictions for inverse functions, the importance of the unit circle for evaluation, and provides practice problems. Finally, it offers exam tips focusing on combining functions and free-response questions.
#AP Pre-Calculus: Inverse Trigonometric Functions - Your Ultimate Study Guide 🚀
Hey there, future AP Pre-Calc master! 👋 Ready to conquer those inverse trig functions? This guide is designed to be your best friend the night before the exam, helping you feel confident and ready. Let's dive in!
#1. Trig Functions: A Quick Review Refresher
Before we jump into inverses, let's make sure we're solid on the basics. Trigonometric functions relate angles to ratios of sides in a right triangle. The main ones are:
- Sine (sin): Opposite / Hypotenuse
- Cosine (cos): Adjacent / Hypotenuse
- Tangent (tan): Opposite / Adjacent
Remember SOH CAH TOA! It's your best friend for remembering these ratios.
#2. Inverse Trigonometric Functions: Unlocking the Angles
Inverse trig functions do the opposite of regular trig functions. Instead of inputting an angle and getting a ratio, you input a ratio and get an angle. These are denoted by "arc" before the trig function name:
- Arcsine (arcsin or sin⁻¹): Finds the angle whose sine is a given value.
- Arccosine (arccos or cos⁻¹): Finds the angle whose cosine is a given value.
- Arctangent (arctan or tan⁻¹): Finds the angle whose tangent is a given value.
#Visualizing Inverse Trig Functions
Here's a quick look at the graphs to help you visualize the functions:

Graph of arcsine. Image courtesy of Math LibreTexts.
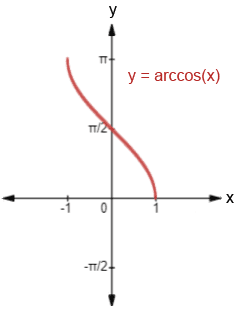
Graph of arccosine. Image courtesy of Math.net.

Graph of arctangent. Image courtesy of Wiktionary.
Notice how the graphs of arcsin and arccos are bounded while arctan extends infinitely. This is due to domain and range restrictions.
#3. Domain and Range Restrictions: The Key to Inverses
Why can't we just use any angle? Because trig functions are periodic, meaning they repeat values. To get unique answers from inverse trig functions, we have to restrict the domains of the original trig functions. Here's the breakdown:
#3.1 Arcsine (sin⁻¹)
- Original Sine Domain Restriction: [-𝛑/2, 𝛑/2]
- Arcsine Range: [-𝛑/2, 𝛑/2] (or [-90°, 90°])
Think of arcsine as only giving you angles on the right side of the unit circle.
#3.2 Arccosine (cos⁻¹)
- Original Cosine Domain Restriction: [0, 𝛑]
- Arccosine Range: [0, 𝛑] (or [0°, 180°])
Think of arccosine as only giving you angles on the top half of the unit circle.
#3.3 Arctangent (tan⁻¹)
- Original Tangent Domain Restriction: (-𝛑/2, 𝛑/2)
- Arctangent Range: (-𝛑/2, 𝛑/2) (or (-90°, 90°))
Arctangent is similar to arcsine, but it never includes -𝛑/2 or 𝛑/2. It's an open interval.
Pay close attention to the brackets ( [ ] ) and parentheses ( ( ) )! Brackets mean the value is included, while parentheses mean it is not.
#4. The Unit Circle: Your Secret Weapon 🎯
The unit circle is incredibly useful for evaluating inverse trig functions. Remember, the input is a ratio, and you're finding the angle. Ask yourself: "What angle gives me this sine/cosine/tangent value?"
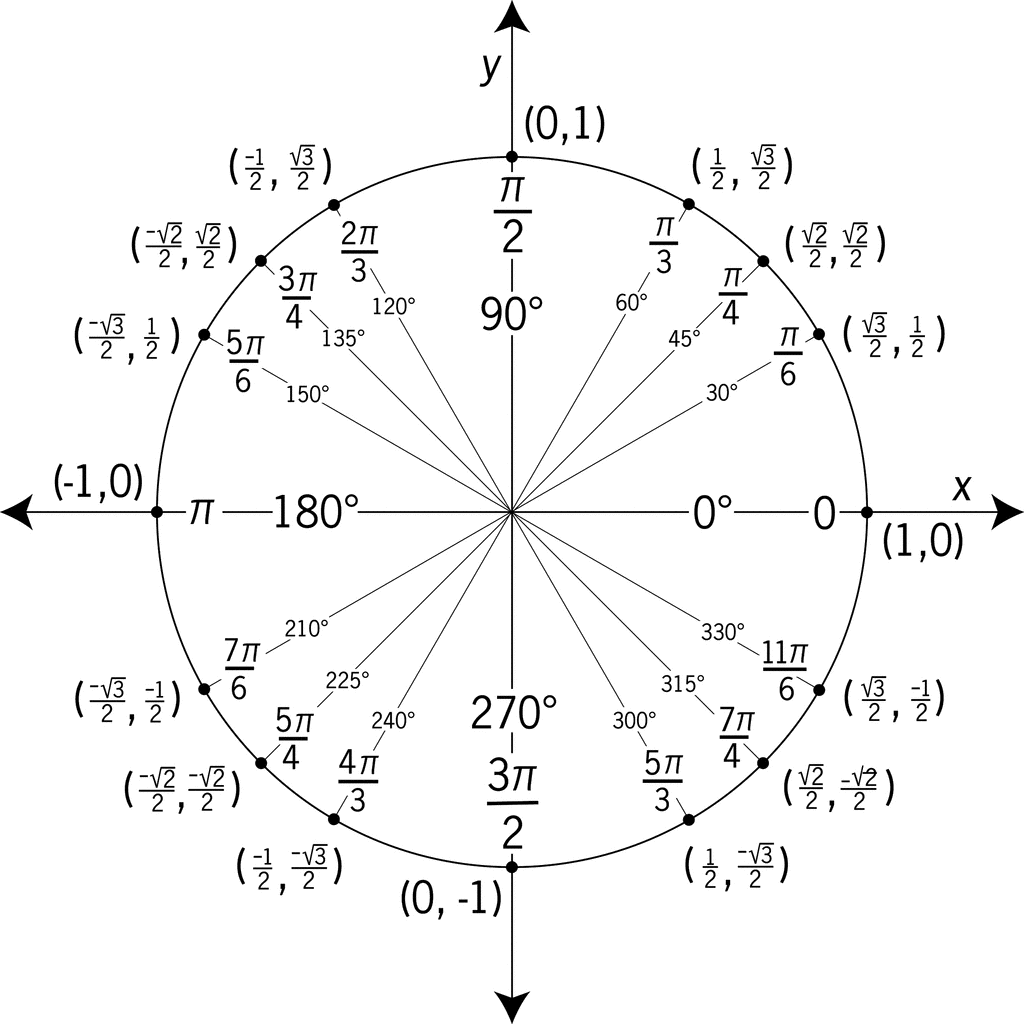
Unit Circle. Image courtesy of Remind.
#Example: arctan(1)
- Question: What angle has a tangent value of 1?
- Look at the Unit Circle: Find where tan = 1 (remember, tan = sin/cos).
- Answer: 𝛑/4 (or 45°), because it falls within the range of arctan.
Mastering the unit circle is crucial. It will save you tons of time on the exam!
#5. Practice Problems: Time to Test Your Skills 💪
Let's solidify your understanding with a few practice questions:
Practice Question
Multiple Choice Questions
-
What is the value of arcsin(-1/2)? a) -30 degrees b) -60 degrees c) 30 degrees d) 60 degrees
-
What is the value of arccos(√2/2)? a) 30 degrees b) 45 degrees c) 60 degrees d) 90 degrees
-
What is the value of arctan(√3)? a) 45 degrees b) 60 degrees c) 90 degrees d) 120 degrees
Answers:
- b) -30 degrees
- b) 45 degrees
- b) 60 degrees
Free Response Question
Evaluate the following expression:
Solution:
- Let . This means .
- Draw a right triangle where the adjacent side is 5 and the hypotenuse is 13. 3. Use the Pythagorean theorem to find the opposite side: , so and .
- Now, find . .
- Therefore,
Scoring Breakdown:
- 1 point for correctly setting up the angle using the arccosine function.
- 1 point for drawing the correct triangle with the given cosine ratio.
- 1 point for using the Pythagorean Theorem to find the missing side.
- 1 point for correctly finding the sine of the angle.
- 1 point for the final answer.
#6. Final Exam Focus: What to Prioritize 🎯
- Domain and Range Restrictions: Make sure you know these for all three inverse functions!
- Unit Circle Mastery: Be able to quickly find angles for common trig values.
- Combining Functions: Practice problems that combine regular trig functions with inverse trig functions.
- FRQ Practice: Be comfortable setting up triangles and using the Pythagorean Theorem.
When you see an inverse trig function, immediately think about the range restrictions!
#7. Last-Minute Tips for Exam Day ⏰
- Time Management: Don't spend too long on one question. If you're stuck, move on and come back.
- Common Pitfalls: Watch out for negative signs and incorrect range values.
- Stay Calm: You've got this! Take deep breaths and trust your preparation.
You're now equipped with the knowledge and strategies to tackle inverse trig functions on the AP Pre-Calculus exam. Go get 'em! 💪
Continue your learning journey

How are we doing?
Give us your feedback and let us know how we can improve





