#Sinusoidal Functions: The Ultimate Guide 🚀

Hey there, future AP Pre-Calculus master! Let's break down sinusoidal functions and make sure you're totally prepped for the exam. This guide is designed to be your go-to resource, especially the night before the test. Let's get started!

#Understanding Sinusoidal Equations

#General Forms

Sinusoidal functions can be expressed in two main forms:

$f(x) = a \sin(b(x + c)) + d$

Or

$f(x) = a \cos(b(x + c)) + d$

Where:

a: Amplitude
b: Frequency (related to the period)
c: Horizontal shift (phase shift)
d: Vertical shift

Key Concept

Key Insight: Both sine and cosine functions produce sinusoidal waves; the choice of sine or cosine often depends on the initial point of the graph. If the graph starts at the midline going up, it's a sine function. If it starts at a maximum, it's a cosine function.

#Constructing Equations from Graphs

Let's dive into how to build these equations from a graph. It's like being a detective, and the graph is our crime scene! 🕵️‍♀️

#Step-by-Step Guide

Consider this graph:

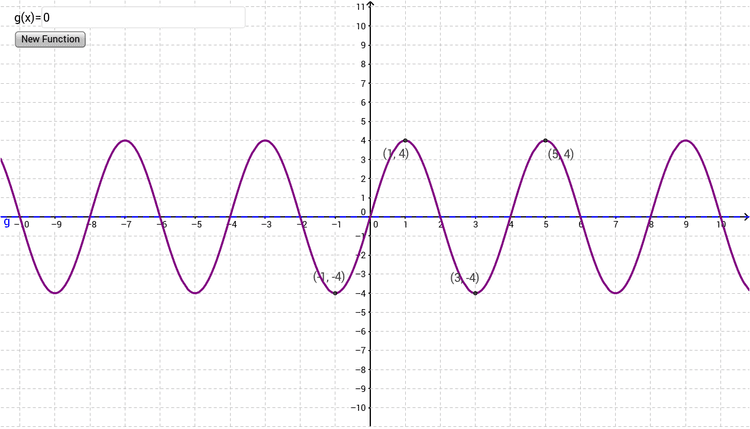
Graph Image

#1. Amplitude (a)

Definition: Half the distance between the maximum and minimum y-values.
Calculation: $amplitude = \frac{|max - min|}{2}$
Example: In the graph above, max = 4, min = -4. So, $amplitude = \frac{|4 - (-4)|}{2} = 4$

#2. Period and Frequency (b)

Period: The horizontal distance it takes for the function to complete one full cycle.
Frequency: Related to the period by $b = \frac{2\pi}{period}$
Example: The graph repeats from x=1 to x=5, so the period = 5 - 1 = 4. Thus, $b = \frac{2\pi}{4} = \frac{\pi}{2}$

#3. Vertical Shift (d)

Definition: The vertical shift of the midline of the function.
Calculation: $midline = \frac{max + min}{2}$ (This is your 'd' value)
Example: In our graph, $midline = \frac{4 + (-4)}{2} = 0$ . So, d = 0. #### 4. Horizontal Shift (c) - Phase Shift
Definition: How much the graph is shifted left or right.
Method: Use a point on the graph and plug it into the equation to solve for 'c'.
Example: Let's use the point (1, 4) and our equation so far: $f(x) = 4\sin(\frac{\pi}{2}(x + c)) + 0$ . Plugging in the point: $4 = 4\sin(\frac{\pi}{2}(1 + c))$ . Solving, we find c = 0.
Memory Aid

Midline Magic: The midline is the average of the max and min values. It's like the 'center' of the wave, and it helps you find the vertical shift (d).

#Putting It All Together

Our equation for the example graph is:

$f(x) = 4\sin(\frac{\pi}{2}x)$

#Practice Problems

Let's put your skills to the test! Here are a few practice problems to solidify your understanding. Remember, practice makes perfect!

#Problem 1

Graph 1

Answer: $f(x) = 5\sin(x + \pi) + 3$

#Problem 2

Graph 2

Answer: $f(x) = 2\sin(x + \frac{\pi}{2}) + 2$

#Problem 3

Graph 3

Answer: $f(x) = 3\sin(3x + \frac{\pi}{3}) + 1$

Exam Tip

Exam Strategy: Always double-check your 'b' value calculation. It's a common spot for errors. Remember, it's tied to the period, not the frequency directly.

#Final Exam Focus

Alright, let's talk about what's most likely to show up on the exam. These are the topics you should absolutely nail down:

Amplitude, Period, and Frequency: Know how to calculate and interpret these from both graphs and equations.
Phase Shift: Be comfortable determining the horizontal shift from a graph.
Vertical Shift: Understand how the midline affects the equation.
Transformations: How do changes in a, b, c, and d affect the graph?

#Common Question Types

Multiple Choice: Identifying parameters from a graph or equation.
Free Response: Constructing the equation of a sinusoidal function from a graph, or vice versa.

#Last-Minute Tips

Time Management: Don't spend too long on one question. If you're stuck, move on and come back later.
Common Pitfalls: Double-check your calculations, especially for 'b' and 'c'. Make sure you're using radians for angles in the sine and cosine functions.
Strategies: Use the process we discussed step-by-step. It will help you stay organized and avoid mistakes.

Quick Fact

Quick Reminder: The period is the horizontal length of one cycle, and the frequency is how many cycles occur in a given unit (usually 2π). They are inversely related.

#

Practice Question

Practice Questions

#Multiple Choice Questions

What is the amplitude of the function $f(x) = -3\sin(2x) + 5$ ? (A) -3 (B) 3 (C) 5 (D) 2
The period of a sinusoidal function is $4\pi$ . What is the value of 'b' in the equation $f(x) = a\sin(bx + c) + d$ ? (A) $4\pi$ (B) $\frac{1}{2}$ (C) $\frac{1}{4}$ (D) 2
A sinusoidal function has a maximum value of 7 and a minimum value of 1. What is the vertical shift (d) of the function? (A) 3 (B) 4 (C) 5 (D) 7

#Free Response Question

Consider the following graph of a sinusoidal function:

FRQ Graph

(a) Determine the amplitude of the function. (1 point) (b) Determine the period of the function. (1 point) (c) Determine the vertical shift of the function. (1 point) (d) Determine the phase shift of the function. (2 points) (e) Write the equation of the sinusoidal function in the form $f(x) = a\sin(b(x + c)) + d$ . (2 points)

Scoring Breakdown:

(a) Amplitude: 3 (1 point) (b) Period: 4 (1 point) (c) Vertical Shift: 1 (1 point) (d) Phase Shift: -1 (2 points) (e) Equation: $f(x) = 3\sin(\frac{\pi}{2}(x + 1)) + 1$ (2 points)

Common Mistake

Watch Out: When calculating the phase shift, make sure you're considering the direction of the shift (left is positive, right is negative) and using radians for the angles.

Remember, you've got this! With a clear understanding of these concepts and a little practice, you'll be well-prepared to tackle any sinusoidal function question on the AP Pre-Calculus exam. Good luck! 🎉