#AP Pre-Calculus: Tangent Functions - Your Ultimate Guide

Hey there, future AP Pre-Calculus master! 👋 Ready to tackle tangent functions? This guide will break it all down, making sure you're totally prepped for the exam. Let's dive in!

#🧭 Constructing the Tangent Function from the Unit Circle

#What is the Tangent Function?

The tangent function, or tan(θ), is a trigonometric function defined as the ratio of the opposite side to the adjacent side in a right triangle. In simpler terms:

tan(θ) = opposite / adjacent = y / x

Image courtesy of Softschools.

#The Unit Circle Connection

Let's revisit our friend, the unit circle: a circle with a radius of 1 centered at the origin. On the unit circle:

• x = cos(θ)

• y = sin(θ)

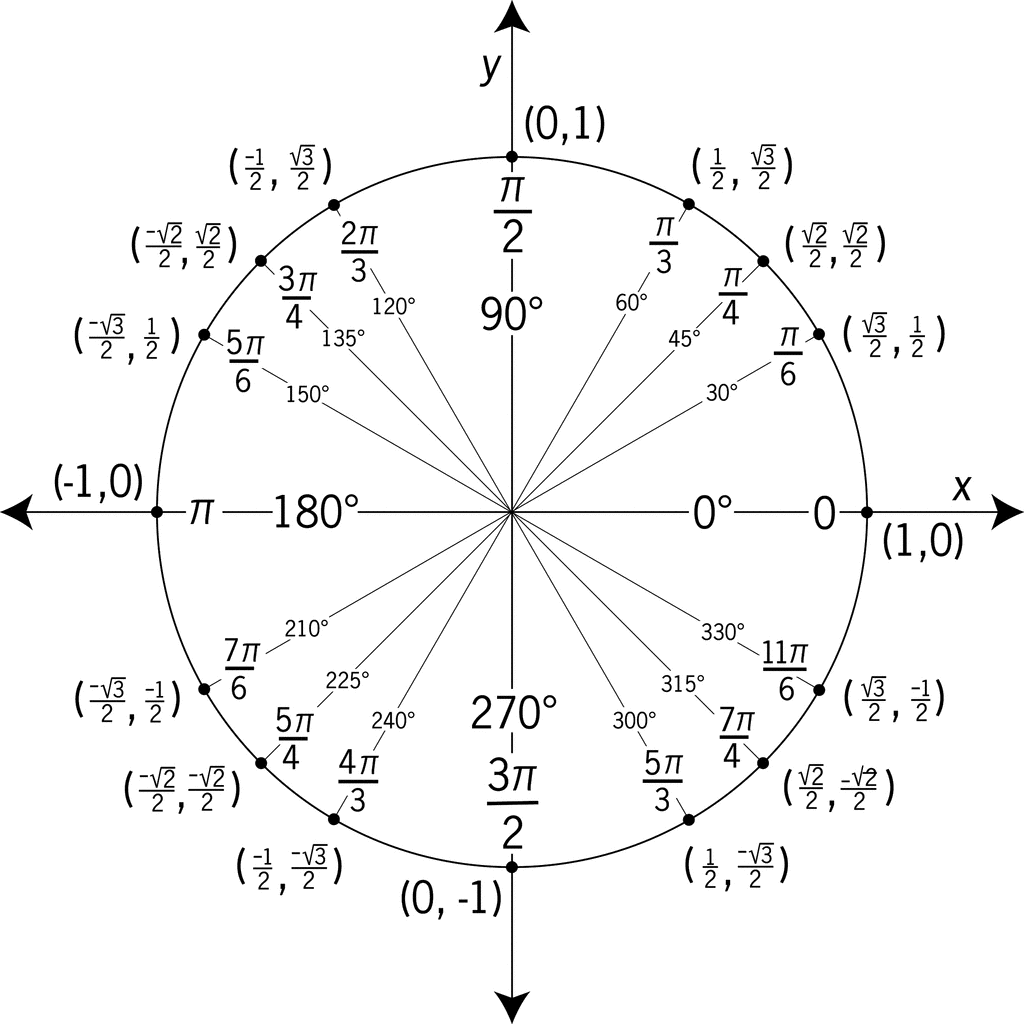
Image courtesy of Remind.

Since tan(θ) = y/x, we can say:

tan(θ) = sin(θ) / cos(θ)

#Tangent's Unique Behavior

Unlike sine and cosine, tangent has some special quirks:

• Vertical Asymptotes: When cos(θ) = 0, tan(θ) is undefined, resulting in vertical asymptotes. This happens at θ = π/2 + kπ, where k is an integer.

• Period of π: Tangent repeats itself every π radians, not 2π like sine and cosine. This is because the slope of the terminal ray repeats every half-rotation of the unit circle.

• Always Increasing: Even though the tangent function resets to negative infinity at each asymptote, it is always increasing.

• Range: The range of tangent is (-∞, ∞), because we can get infinitely close to zero in the denominator without actually reaching it.

Image courtesy of Wolfram MathWorld.

#📈 Transformations of the Tangent Function

#The General Equation

Just like sinusoidal functions, tangent functions can be transformed using the general equation:

y = a tan(b(x - c)) + d

Image courtesy of CollegeBoard.

Here's what each part does:

• a (Amplitude): Controls the vertical dilation. If 'a' is negative, the function is reflected over the x-axis.

• b (Period): Affects the period of the function. The period is T = π/b. A smaller 'b' means a wider graph and a larger period.

• c (Phase Shift): Shifts the graph horizontally. Positive 'c' shifts right, negative 'c' shifts left.

• d (Vertical Shift): Shifts the graph vertically. Positive 'd' shifts up, negative 'd' shifts down.

#🎯 Final Exam Focus

#Key Topics to Master

• Understanding the Unit Circle: Know how sine, cosine, and tangent relate to the unit circle.
• Tangent Function Basics: Understand its period, asymptotes, and range.
• Transformations: Be able to identify and apply vertical dilations, reflections, phase shifts, and vertical shifts.
• Period Calculation: Master the period formula: T = π/b.

#Common Question Types

• Multiple Choice: Expect questions on identifying the period, asymptotes, and transformations of tangent functions.
• Free Response: Be prepared to graph transformed tangent functions and write equations from given graphs.
• Application Questions: Apply your knowledge of tangent functions to real-world scenarios.

#Last-Minute Tips

• Time Management: Don't spend too long on one question. If you're stuck, move on and come back later.
• Common Pitfalls: Be careful with negative signs and remember the period of tangent is π, not 2π.
• Strategies: Draw a quick sketch of the unit circle to help visualize the tangent function's behavior.

Focus on transformations and period calculations, as they are frequently tested.

#📝 Practice Questions

Practice Question

#Multiple Choice Questions

1. What is the period of the function y = tan(2x)? (A) π/4 (B) π/2 (C) π (D) 2π

2. The graph of y = tan(x) has vertical asymptotes at which of the following values of x? (A) kπ, where k is an integer (B) π/2 + kπ, where k is an integer (C) 2kπ, where k is an integer (D) π/4 + kπ, where k is an integer

3. Which transformation is applied to the graph of y = tan(x) to obtain the graph of y = -tan(x)? (A) Vertical shift (B) Horizontal shift (C) Reflection over the x-axis (D) Reflection over the y-axis

#Free Response Question

Consider the function f(x) = 2 tan(x/2) - 1. (a) State the period of the function.

(b) State the vertical asymptotes of the function in the interval [-2π, 2π].

(c) Sketch the graph of the function on the interval [-2π, 2π].

Scoring Rubric:

(a) Period (2 points):

• 1 point: Correctly using the formula T = π/b
• 1 point: Correct period of 2π

(b) Vertical Asymptotes (3 points):

• 1 point: Correctly identifying the form of vertical asymptotes: x = π + 2kπ
• 1 point: Correctly identifying asymptotes at x = -π and x = π.
• 1 point: Correctly identifying asymptotes at x = -3π and x = 3π.

(c) Graph (4 points):

• 1 point: Correct general shape of tangent function
• 1 point: Correct placement of vertical asymptotes
• 1 point: Correct vertical stretch
• 1 point: Correct vertical shift

That's it! You're now equipped to conquer tangent functions on the AP Pre-Calculus exam. Keep practicing, stay confident, and you've got this! 💪