#AP Pre-Calculus: Matrices - Your Night-Before Review 🚀

Hey there! Let's get you feeling super confident about matrices for your AP Pre-Calculus exam. This guide is designed to be quick, clear, and exactly what you need for a last-minute review. Let's dive in!

#What are Matrices?

A matrix is like a table of numbers, symbols, or expressions arranged in rows ↔️ and columns ↕️. Think of it as a super-organized spreadsheet, but instead of just holding data, we use it for math operations like solving equations, finding determinants, and doing transformations. ⚙️

Matrix Example

A visual representation of a matrix.

Memory Aid

Think of a matrix as a toolbox 🧰. Each element is like a tool, and you use them to perform different mathematical tasks.

#Notation ✍️

Just like a toolbox has a specific size, a matrix is described by its dimensions: the number of rows and columns. An n x m matrix has n rows and m columns. Each element's position is given by its row and column number. 🧱

#Matrix Multiplication *️⃣

Key Concept

Matrix multiplication isn't just multiplying numbers straight across. It has a specific rule: the number of columns in the first matrix must equal the number of rows in the second matrix. This is the matrix compatibility rule. 📏

Matrix Multiplication Compatibility

Two matrices can be multiplied if the inner dimensions match.

If matrix A is n x m and matrix B is m x p, then their product C = A x B is an n x p matrix. The element in the ith row and jth column of C is the dot product of the ith row of A and the jth column of B. ✅

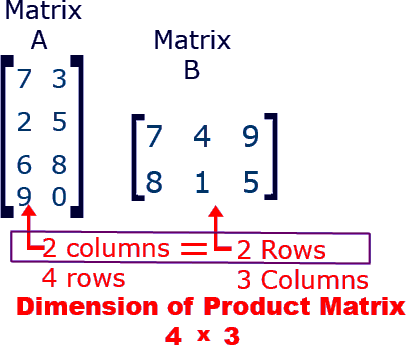
Dimension of product matrix

The resulting matrix has dimensions equal to the outer dimensions of the original matrices.

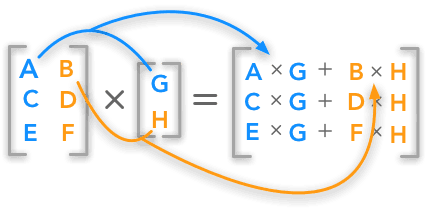
Matrix Multiplication Example

A visual example of how matrix multiplication is performed.

#Dot Product 🧐

The dot product (or scalar product) is how we multiply two vectors to get a single number (a scalar). 💠

Quick Fact

The dot product is commutative: A • B = B • A. 🔄

To find the dot product, multiply corresponding components of the two vectors and then add up the results. It’s like multiplying each direction separately and then adding them together. 👁

For example, if A = [3, 4] and B = [2, 1]:

A • B = (3 * 2) + (4 * 1) = 6 + 4 = 10

Memory Aid

Think of the dot product as a way to see how much two vectors are pointing in the same direction. 💡

#Final Exam Focus 🎯

Here's what to prioritize for your exam:

Matrix Multiplication: Make sure you're comfortable with the compatibility rule and how to calculate the product of two matrices. This is a high-value topic.
Dot Product: Know how to compute it and its properties. It’s often used in more complex matrix problems.

Key Concept

Matrix Dimensions: Understand how matrix dimensions affect operations.

Quick Fact

#Last-Minute Tips ⏱️

Time Management: Don't spend too long on one question. If you're stuck, move on and come back later.

Exam Tip

Common Mistakes: Double-check your calculations, especially in matrix multiplication. It's easy to make mistakes with so many numbers.

Common Mistake

Read Carefully: Pay attention to the specific instructions in each problem. AP questions often have little twists.

Exam Tip

#Practice Questions

Practice Question

Multiple Choice Questions

Given matrices A = [[1, 2], [3, 4]] and B = [[5, 6], [7, 8]], what is the element in the first row and first column of the product AB? (A) 19 (B) 22 (C) 23 (D) 53
If matrix P is a 3x2 matrix and matrix Q is a 2x4 matrix, what are the dimensions of the resulting matrix when P is multiplied by Q? (A) 2x2 (B) 3x4 (C) 4x3 (D) 2x3

Free Response Question

Consider the following matrices:

A = [[2, -1], [3, 0]] and B = [[1, 4], [-2, 1]]

(a) Calculate the product AB. (b) Calculate the product BA. (c) Is matrix multiplication commutative in this case? Explain.

Scoring Rubric:

(a) 2 points: 1 point for correct setup, 1 point for correct result. AB = [[21 + (-1)(-2), 24 + (-1)1], [31 + 0(-2), 34 + 01]] = [[4, 7], [3, 12]]

(b) 2 points: 1 point for correct setup, 1 point for correct result. BA = [[12 + 43, 1*(-1) + 40], [(-2)2 + 13, (-2)(-1) + 1*0]] = [[14, -1], [-1, 2]]

You've got this! Go ace that exam! 🎉