#AP Calculus AB/BC: Limits at Infinity & Horizontal Asymptotes 🚀

Hey there, future AP Calculus master! Let's nail down limits at infinity and horizontal asymptotes. This is a crucial topic, and by the end of this guide, you'll be feeling super confident. Let's dive in!

#1.15 Connecting Limits at Infinity and Horizontal Asymptotes

This section is all about how functions behave as x gets super big (or super small). We're talking about what happens way, way out on the graph.

# 🔍 Review: Limits to Infinity

Remember, a limit is what a function's y-value approaches as x approaches a certain value. When we say "x approaches infinity (∞) or negative infinity (-∞)," we're looking at the function's end behavior.

$$\lim_{x \to \infty} f(x)$$ $$\lim_{x \to -\infty} f(x)$$

# 🧐 Finding Limits to Infinity

The key to finding limits at infinity? Horizontal Asymptotes (HAs)! Think of HAs as the "speed limit" for a function's y-values. 🚦

# 🚥 Horizontal Asymptotes

A horizontal asymptote is a y-value that the graph approaches but never actually touches or crosses (at least not at the extreme ends). It's like a finish line the function tries to reach but never quite gets to. 🛑

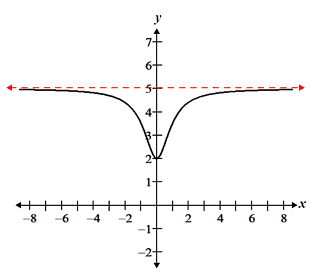
Image Courtesy of MATH.net

Caption: The graph shows a function with a horizontal asymptote at y = 5. Notice how the function gets closer and closer to y = 5 as x goes to infinity, but never actually touches it.

In this graph, the horizontal asymptote is at y = 5. So, we can say: $\lim_{x \to \infty} f(x) = 5$.

# 🔍 Finding Horizontal Asymptotes

Here's the lowdown on finding HAs for rational functions (functions that are fractions of polynomials): Let's think of a function as $\frac{p(x)}{q(x)}$.

Examples:

🥇 $\lim_{x \to \infty} \frac{4x+2}{3x^2+1} = 0$ (Bottom wins!)

🥈 $\lim_{x \to \infty} \frac{4x^2+2}{3x+1} = \infty$ (Top wins!)

🥉 $\lim_{x \to \infty} \frac{3x^2+2}{4x^2+1} = \frac{3}{4}$ (Coefficients battle it out!)

#Exceptions to These Rules

• Oscillating Functions: The limit of an oscillating function at infinity does not exist. 🎢
  • Ex: $\lim_{x \to \infty} \sin(x) = DNE$
• Squeeze Theorem: Any function that is part of the squeeze theorem will equal 0 as it approaches infinity. 🥪
  • Ex: $\lim_{x \to \infty} \frac{\sin(x)}{x} = 0$

# 🌱 The Growth Rates of Functions

Different functions grow at different speeds! Knowing this can be super helpful. Here's the growth rate hierarchy from slowest to fastest: 🪴

log < root < polynomial < exponential

---

# ✏️ Infinite Limits & Horizontal Asymptotes Practice

Let's put this knowledge to work with some examples!

#Infinite Limits: Example 1

Evaluate: $\lim_{x \to \infty} \frac{3x-1}{e^x}$

• The denominator, e^x, is an exponential function, which grows much faster than the numerator, 3x - 1. So, we have a $\frac{\text{small number}}{\text{large number}}$ situation.
• Therefore, $\lim_{x \to \infty} \frac{3x-1}{e^x} = 0$.

#Infinite Limits: Example 2

Evaluate: $\lim_{x \to \infty} \frac{2^x}{x-5}$

• Here, the exponential function, 2^x, is in the numerator, which grows much faster than the denominator, x - 5. So, we have a $\frac{\text{large number}}{\text{small number}}$ situation.
• Therefore, $\lim_{x \to \infty} \frac{2^x}{x-5} = \infty$.

# 🎯 Final Exam Focus

• High-Priority Topics: Limits at infinity, horizontal asymptotes, growth rates of functions. These appear in both MCQs and FRQs.
• Common Question Types: Finding HAs of rational functions, evaluating limits involving exponential and logarithmic functions, applying the squeeze theorem.
• Time Management: Quickly identify the degrees of polynomials and growth rates of functions to save time on MCQs.
• Common Pitfalls: Forgetting to consider growth rates, misapplying HA rules, not recognizing oscillating functions.
• Strategies: Always simplify before evaluating limits, think about the relative growth rates of functions, and remember your HA rules!

# 📝 Practice Questions

Practice Question

Multiple Choice Questions

1. $\lim_{x \to \infty} \frac{5x^3 - 2x + 1}{2x^3 + 7x^2 - 4}$ is equal to: (A) 0 (B) 5/2 (C) ∞ (D) 2/5

2. $\lim_{x \to \infty} \frac{4x + \sin(x)}{x}$ is equal to: (A) 0 (B) 4 (C) ∞ (D) DNE

3. $\lim_{x \to \infty} \frac{\ln(x)}{x^2}$ is equal to: (A) 0 (B) 1 (C) ∞ (D) DNE

Free Response Question

Consider the function $f(x) = \frac{3x^2 - 5}{x^2 + 2x}$.

(a) Find all horizontal asymptotes of f(x).

(b) Evaluate $\lim_{x \to \infty} f(x)$.

(c) Evaluate $\lim_{x \to -\infty} f(x)$.

(d) Does the function have any vertical asymptotes? If so, find them.

Answer Key

Multiple Choice

1. (B) The degrees are equal, so the limit is the ratio of the coefficients: 5/2. 2. (B) Divide each term by x, $\lim_{x \to \infty} 4 + \frac{\sin(x)}{x} = 4 + 0 = 4$.
2. (A) The denominator grows faster than the numerator, so the limit is 0. Free Response

(a) The horizontal asymptote is y = 3, since the degrees are equal, the limit is the ratio of the coefficients: 3/1 = 3. (b) $\lim_{x \to \infty} f(x) = 3$ (same as the horizontal asymptote).

(c) $\lim_{x \to -\infty} f(x) = 3$ (same as the horizontal asymptote).

(d) Yes, vertical asymptotes occur where the denominator is zero: $x^2 + 2x = 0 \implies x(x+2) = 0$. Thus, the vertical asymptotes are at x = 0 and x = -2. Scoring Breakdown for FRQ

• (a) 1 point for stating the horizontal asymptote y = 3. * (b) 1 point for stating the correct limit as x approaches infinity.
• (c) 1 point for stating the correct limit as x approaches negative infinity.
• (d) 1 point for identifying the vertical asymptotes at x = 0 and x = -2.

You got this! Keep practicing, and you'll be a pro in no time. Let's ace that exam! 💪