#AP Microeconomics: Income Inequality - The Final Frontier!

YOU MADE IT!!! 🎉 You've conquered supply and demand, monopolies, game theory, and more! Now, let's tackle the final piece: income inequality. This unit is crucial for understanding how markets can fail and how we measure and address inequality. Let's dive in!

#Types of Inequality

There are two main types of economic inequality:

• Income Inequality: How annual earnings are distributed.

• Wealth Inequality: How assets are distributed.

#The Lorenz Curve

The Lorenz Curve is a visual tool to represent income inequality. It plots the cumulative percentage of income against the cumulative percentage of the population. The further the curve is from the line of perfect equality, the greater the inequality. 💡

Gini Coefficient: A numerical measure of income inequality, ranging from 0 (perfect equality) to 1 (perfect inequality). It's calculated as the ratio of the area between the line of perfect equality and the Lorenz curve (Area A) to the total area under the line of perfect equality (Area A + B).

$$Gini\ Coefficient = \frac{A}{A+B}$$

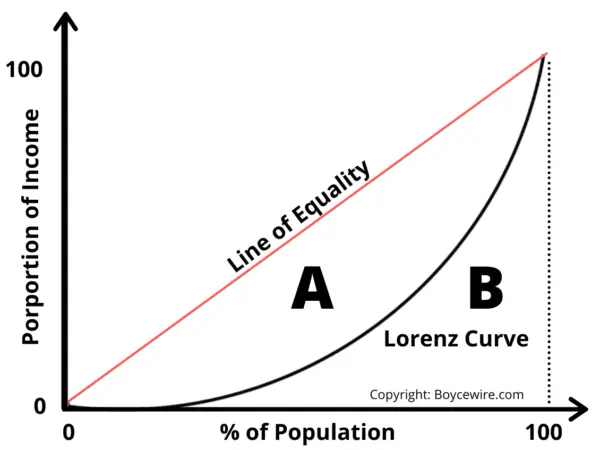
A higher Gini coefficient means greater income inequality. The world average Gini Coefficient is between 0.61 and 0.68.

#Types of Taxes

Taxes can either worsen or mitigate income inequality. Let's break down the main types:

• Progressive Taxes: Take a larger percentage of income from high-income groups. ⬆️
  • Example: Federal Income Tax in the U.S. (higher income = higher tax rate).
    
• Regressive Taxes: Take a larger percentage from low-income groups. ⬇️
  • Example: Sales tax. Even though everyone pays the same rate, it's a larger burden for those with lower incomes.

- **Proportional Taxes**: Take the same percentage of income from all income groups. ⚖️ - Example: A flat income tax where everyone pays the same percentage.

Understanding the Lorenz curve, Gini coefficient, and the different types of taxes is crucial for the exam. Be ready to analyze how these concepts relate to income inequality.

#Final Exam Focus

• Lorenz Curve & Gini Coefficient: Be able to draw a Lorenz curve, explain what it represents, and calculate the Gini coefficient. Understand how changes in income distribution affect the curve and the Gini coefficient.

• Tax Systems: Know the difference between progressive, regressive, and proportional taxes. Understand how each affects income distribution and equity.

• Market Failure: Understand that income inequality is a form of market failure and how the government can intervene to address it.

Practice Question

#Practice Questions

Multiple Choice Questions

1. Which of the following best describes a regressive tax? (A) A tax that takes a larger percentage of income from high-income earners. (B) A tax that takes a larger percentage of income from low-income earners. (C) A tax that takes the same percentage of income from all income earners. (D) A tax that is only applied to luxury goods. (E) A tax that is not applied to essential goods.

2. A country's Lorenz curve shifts further away from the line of perfect equality. This indicates: (A) A decrease in income inequality. (B) An increase in income equality. (C) An increase in income inequality. (D) No change in income inequality. (E) A decrease in the Gini coefficient.

3. Which of the following is NOT a source of economic inequality? (A) Differences in human capital (B) Inheritance (C) Government transfer payments (D) Discrimination (E) Access to financial markets

Free Response Question

Assume a hypothetical economy with the following income distribution:

Income Group	Percentage of Population	Percentage of Total Income
Lowest 20%	20%	5%
Second 20%	20%	10%
Middle 20%	20%	15%
Fourth 20%	20%	25%
Highest 20%	20%	45%

(a) Draw a fully labeled Lorenz curve for this economy. Be sure to label the axes and the line of perfect equality. (b) Calculate the Gini coefficient for this economy. Show your work. (c) Suppose the government implements a progressive tax system. Explain how this would affect the Lorenz curve and Gini coefficient.

Answer Key

Multiple Choice

1. (B)
2. (C)
3. (C)

Free Response Question

(a) Lorenz Curve

• X-axis: Cumulative percentage of the population (2 points)
• Y-axis: Cumulative percentage of income (2 points)
• Line of perfect equality: Straight diagonal line (1 point)
• Lorenz curve: Plotted correctly based on the given data (2 points)

(b) Gini Coefficient

• Area A: Calculate the area between the perfect equality line and the Lorenz curve. This can be done by finding the area under the perfect equality line (0.5) and subtracting the area under the Lorenz curve. (2 points)
• Area B: Calculate the area under the Lorenz curve (0.25)
• Gini Coefficient: A / (A + B) = 0.25 / 0.5 = 0.5 (2 points)

(c) Progressive Tax Impact

• Lorenz Curve: The Lorenz curve would shift closer to the line of perfect equality (1 point)
• Gini Coefficient: The Gini coefficient would decrease (1 point)
• Explanation: A progressive tax system takes a larger percentage of income from higher earners and redistributes it to lower earners, resulting in a more equal income distribution (2 points)

You've got this! Remember to stay calm, focus on the key concepts, and trust your preparation. Good luck on the exam! 💪