Free-Body Diagrams for Objects in Uniform Circular Motion
Joseph Brown
8 min read
Listen to this study note
Study Guide Overview
This study guide covers free body diagrams (FBDs) and their application to uniform circular motion. It explains how to draw and interpret FBDs, emphasizing the importance of the coordinate system and including common forces like gravity, tension, friction, and normal force. The guide uses a roller coaster case study to illustrate FBDs at different points in a loop, highlighting the relationship between normal force and apparent weight. Finally, it provides practice questions and exam tips focused on applying Newton's Second Law in circular motion scenarios.
#AP Physics 1: Free Body Diagrams & Circular Motion - The Ultimate Study Guide 🎢
Hey there, future AP Physics master! Let's break down Free Body Diagrams (FBDs) and circular motion. This guide is designed to be your go-to resource the night before the exam. Let's get started!
#1. Free Body Diagrams (FBDs) Basics 🎯
#What's an FBD?
- A free body diagram (FBD) is a visual tool that shows all the forces acting on an object. It helps us analyze motion, especially in scenarios like uniform circular motion. Think of it as a force map! 🗺️
#How to Draw FBDs
- Method 1 (Point Mass): Represent the object as a dot and draw arrows outward from the dot to represent forces. This is what we'll use in this guide.
- Method 2 (Detailed): Draw forces at the specific points where they are exerted on the object. Useful for more complex analysis.
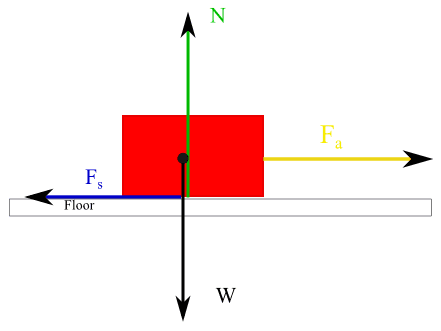
In the image above, notice how each force is drawn at the point it acts on the box: friction at the contact point, weight at the center of mass, and the applied force at the point of contact.
Remember, the weight force (W) always acts at the center of mass, pointing downwards towards the Earth.
#Coordinate System
-
Always choose a coordinate system where the positive x or y axis points towards the center of the circle. This simplifies your analysis of centripetal force. 💡
Always align your axes such that the centripetal force is along one of the axes. This will make your calculations much easier.
#2. FBDs for Uniform Circular Motion 🔄
#Key Idea
- In uniform circular motion, the net force (centripetal force) always points towards the center of the circle. This force is what causes the object to move in a circular path.
#Gravity and Centripetal Force
- The gravitational force doesn't always point downwards. For example, in a planet's orbit, gravity acts as the centripetal force, pointing toward the center of the o...
How are we doing?
Give us your feedback and let us know how we can improve