#AP Physics C: Mechanics - Rotational Motion Study Guide 🚀

Hey there, future physics pro! Let's get you prepped for the AP exam with a deep dive into rotational motion. This guide is designed to be your go-to resource, especially the night before the test. Let's make sure you feel confident and ready to ace it!

#1. Rotational Dynamics & Equilibrium

#1.1. Rotational Dynamics

Key Concept

Rotational Dynamic Equilibrium: This is the rotational version of Newton's Second Law. When the net torque on an object is zero, it is in rotational equilibrium. The sum of the net torques is equal to the rotational inertia times the angular acceleration.

$\sum \tau_{net} = I \alpha$

Where:

$\tau$ is torque
$I$ is the moment of inertia
$\alpha$ is the angular acceleration

Torque ( $\tau$ ): The 'twisting force' that causes rotation. Remember, the further the force is from the axis of rotation, the greater the torque. Think of it like using a longer wrench to loosen a bolt – more leverage, more torque!

#1.2. Rigid Body Diagrams

Just like free-body diagrams (FBDs) for linear motion, we have rigid body diagrams for rotational motion. These diagrams show where forces are applied to an object, which is crucial for calculating torques.

How to Draw a Rigid Body Diagram: 1. Identify the object and its reference frame (origin and axes). 2. Draw the forces acting on the object as vectors, with the tail at the point of application and the arrow in the direction of the force. Examples include weight, friction, tension, and normal forces. 3. Draw the moments (torques) acting on the object as vectors, with the tail at the point of application and the arrow in the direction of the moment. 4. Label all vectors with their magnitude and direction. 5. Sum the forces and moments to find the net force and net moment.
Key Difference from FBDs: Rigid body diagrams show where forces are applied, which is essential for calculating torques.
Visual Aid:

Rigid Body Diagram

Caption: Example of a rigid body diagram showing force vectors applied at different points on an object.

Exam Tip

Always use force diagrams and equations in conjunction with torque calculations. They are often interconnected in problems.

#2. Rolling, Sliding, and Rotating

#2.1. Rolling Motion

When an object is rolling (without slipping), the frictional force does no work. This is a crucial point! In such cases, we can often use the conservation of mechanical energy. 💡

Rolling vs. Sliding: * Rolling: Object rotates and translates without slipping (friction does no work). * Sliding: Object translates without rotating (friction does work).

#2.2. Race Down the Ramp

Let's consider a classic scenario: a box, a hoop, and a ball released simultaneously at the top of a ramp.

Frictionless Ramp: * All three objects will reach the bottom at the same time. Why? Because they are all subject to the same gravitational force, and there's no friction to slow them down differently. They accelerate vertically downward at the same rate, regardless of their shape or size. Each object will follow a different trajectory based on their individual shapes and characteristics. The box will move vertically down, while the hoop will roll down and the ball will move in a parabolic trajectory. But, all will reach the bottom at the same time as they are subject to the same gravitational force.
Ramp with Friction: * Things change with friction! The order of arrival will be: ball (first), then hoop, and lastly the box. Here's why:
- Box: Slides down, experiencing kinetic friction, which slows it down the most.
- Hoop: Rolls down, experiencing less friction than the box. Some energy is converted to rotational kinetic energy.
- Ball: Rolls down with the least amount of friction due to its shape and mass distribution. More of its energy goes into rotational kinetic energy.

Memory Aid

Think of it like this: the object that converts more of its potential energy into rotational kinetic energy will reach the bottom first because it's using energy to roll instead of just sliding and fighting friction. The ball is the most efficient at this. ⚽

#3. Rotational Energy

Just like objects can have translational kinetic energy, they can also have rotational kinetic energy! Most of the time, you'll see a combination of both.

Definition: Rotational energy is the energy an object has due to its rotation around an axis.
Formula: $KE_{rot} = \frac{1}{2} I \omega^2$ Where: - $KE_{rot}$ is rotational kinetic energy - $I$ is the moment of inertia - $\omega$ is the angular velocity
Key Points: * The moment of inertia ( $I$ ) is the measure of an object's resistance to rotational motion. It depends on how mass is distributed around the axis of rotation. * Angular velocity ( $\omega$ ) is the rate of change of angular displacement. * Rotational energy is a scalar quantity. * Rotational energy increases with angular velocity and moment of inertia. * It's a form of kinetic energy and can be converted into other forms of energy.
Visual Aid:

Rotational Energy

Caption: Illustration of rotational kinetic energy, showing the relationship between angular velocity and moment of inertia.

Rotational energy is a high-value topic. Expect to see questions that combine rotational and translational kinetic energy, as well as the conservation of energy.

#4. Final Exam Focus 🎯

Okay, let's talk about what's most likely to show up on the exam. Here’s your last-minute checklist:

High-Priority Topics: * Rotational Dynamics: Know how to apply $\sum \tau = I \alpha$ and understand the relationship between torque, moment of inertia, and angular acceleration. * Rigid Body Diagrams: Practice drawing them accurately, paying close attention to where forces are applied. * Rolling Motion: Understand the difference between rolling and sliding, and how friction affects motion on an incline. * Rotational Energy: Master the formula $KE_{rot} = \frac{1}{2} I \omega^2$ and how it relates to total mechanical energy. * Conservation of Energy: Be ready to apply the principle of conservation of energy in scenarios involving both translational and rotational motion.
Common Question Types: * Multiple Choice: Conceptual questions about which objects reach the bottom of a ramp first, or how different forces affect rotational motion. * Free Response: Problems that require you to draw rigid body diagrams, calculate torques, and apply conservation of energy principles.
Last-Minute Tips: * Time Management: Don't spend too long on one question. If you're stuck, move on and come back later. * Common Pitfalls: Watch out for mixing up translational and rotational variables. Make sure your units are consistent. * Strategies: Draw clear diagrams and write down all equations before you start solving. This will help you stay organized and avoid mistakes.

Exam Tip

Remember to always check your units and make sure your answers make sense in the context of the problem. For example, a moment of inertia should not be negative.

#5. Practice Questions

Practice Question

Multiple Choice Questions:

Question:

Answer:
Question:

Answer:
Question:

Answer:

Free Response Question:

Question:

  ![FRQ](https://zupay.blob.core.windows.net/resources/files/0baca4f69800419293b4c75aa2870acd_6415c9_1747.png?alt=media&token=ce5ec803-1588-49a1-8491-ad26c9cd2212)

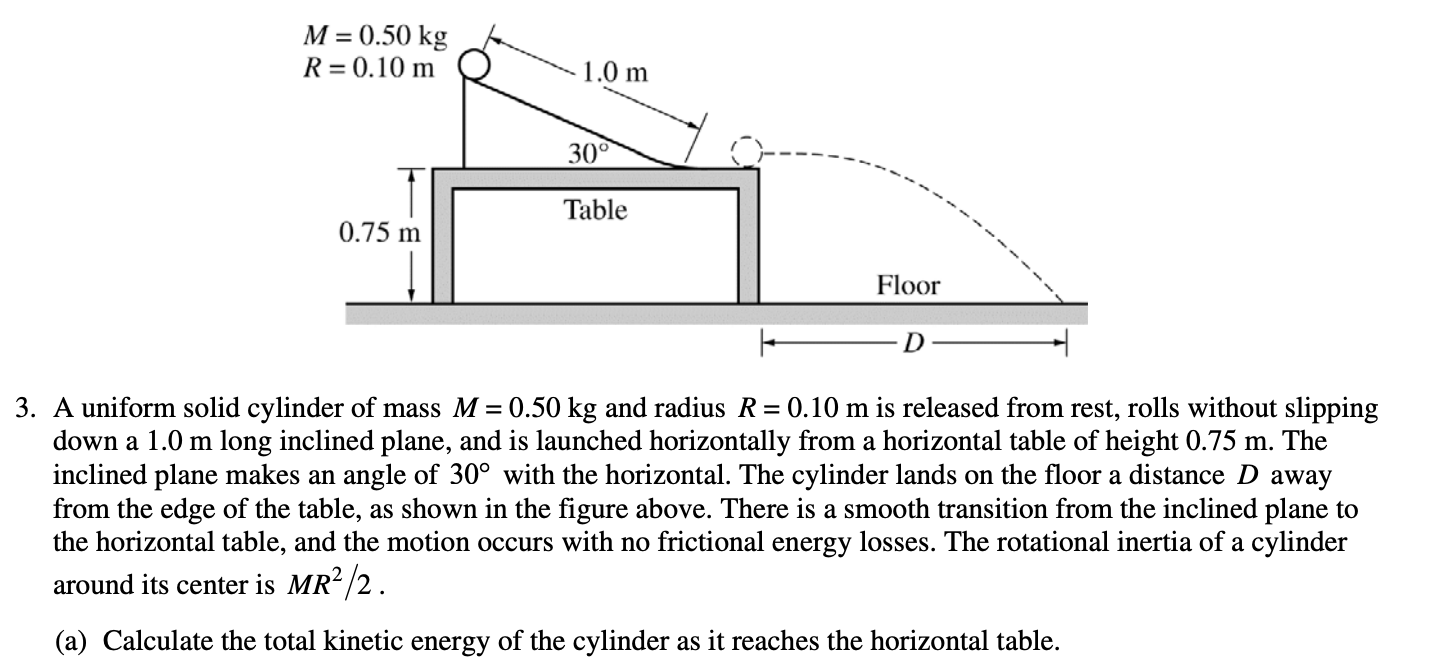
Answer:

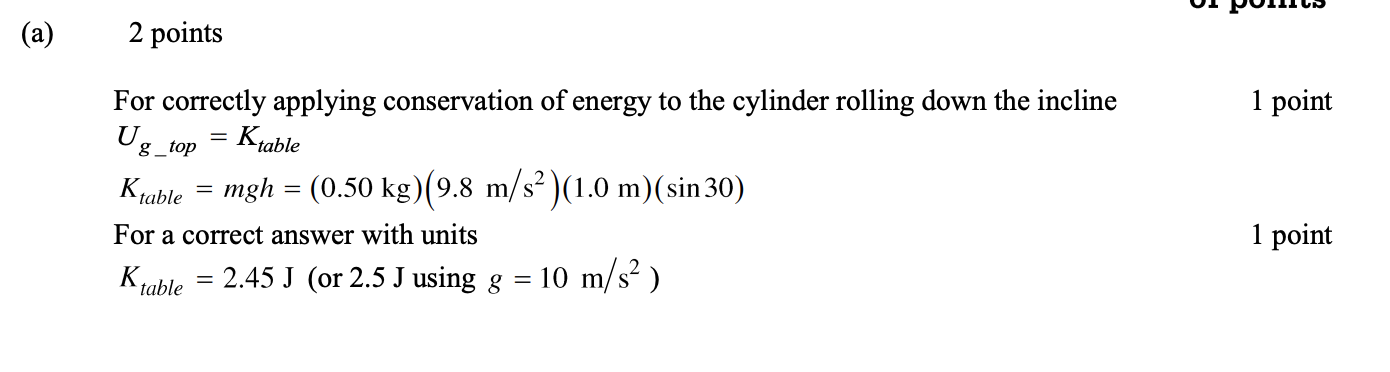
  ![Answer FRQ](https://zupay.blob.core.windows.net/resources/files/0baca4f69800419293b4c75aa2870acd_50b75d_1530.png?alt=media&token=e591ffe8-9fa5-4390-b51d-39ca4a899597)

Combined Concepts Question:

Question:

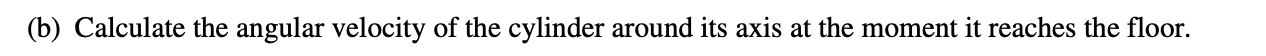
  ![Combined Question](https://zupay.blob.core.windows.net/resources/files/0baca4f69800419293b4c75aa2870acd_05b769_1502.png?alt=media&token=0bef29c9-a26e-4dfa-ad87-c91949ad5c39)

Answer:

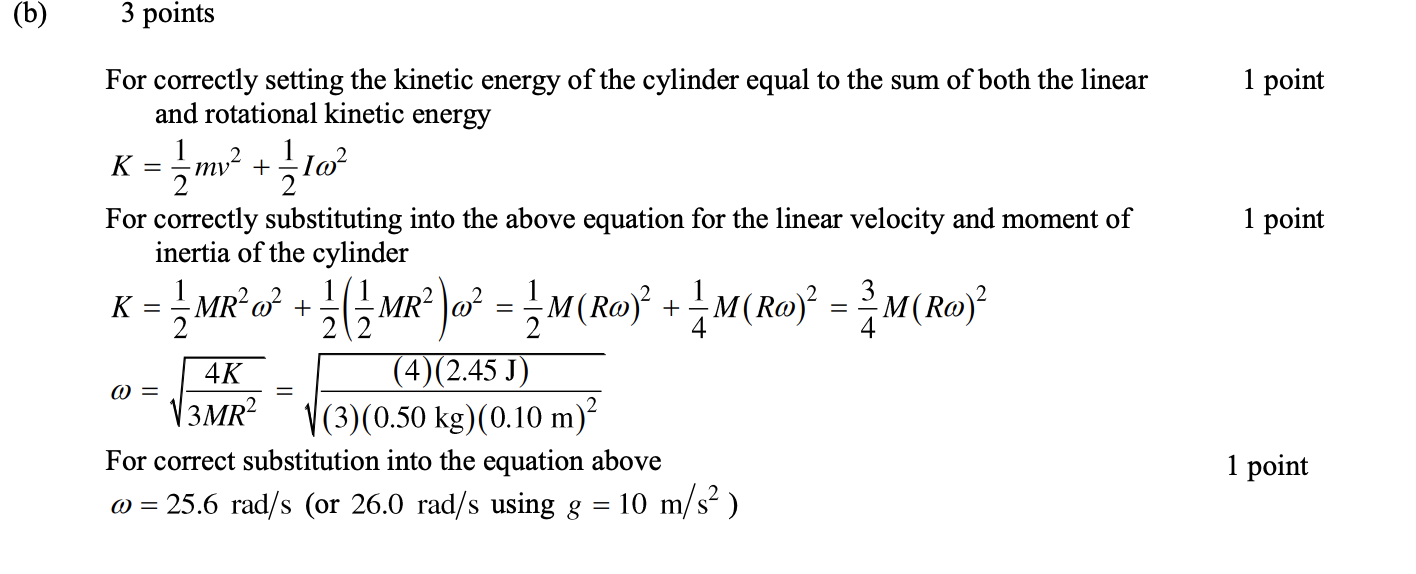
  ![Answer Combined Question](https://zupay.blob.core.windows.net/resources/files/0baca4f69800419293b4c75aa2870acd_3ce513_2279.png?alt=media&token=ed97f966-9967-49a1-8d35-7bdf9400617b)

You've got this! Remember to breathe, stay calm, and trust in your preparation. Good luck on the exam! 🎉