#AP Physics C: Mechanics - Potential Energy Study Guide 🚀

Hey there, future AP Physics C champ! Let's dive into potential energy, a core concept that'll unlock a lot of mechanics problems. This guide is designed to be your go-to resource, especially when you're reviewing the night before the exam. Let's make sure you're feeling confident and ready to ace it!

#Potential Energy: The Basics

Potential energy is all about stored energy within a system due to the positions of its components. It's like the system's potential to do work. Remember, it's a scalar quantity, meaning it has magnitude but no direction. Let's break it down:

#Conservative Forces and Potential Energy

• Conservative Forces: These are forces where the work done is independent of the path taken. Think of it like this: if you move an object in a closed loop, the net work done by a conservative force is zero. Examples include:
  • Gravity
  • Electrostatic forces
  • Elastic spring forces
• Non-Conservative Forces: These forces, like friction and air resistance, dissipate energy as heat and do not have an associated potential energy.

• Potential energy (U) is a scalar, meaning it only has magnitude, no direction.
• It depends on the relative positions of objects within a system.
• The change in potential energy (ΔU) is what matters, not the absolute value. It's determined by the start and end points, not the path taken.

#Defining Zero Potential Energy

• The zero point for potential energy is arbitrary and chosen for convenience. It's like setting a reference point for a height measurement.
• Common choices:
  • Gravitational: Ground level (U = 0 at y = 0)
  • Elastic: Equilibrium position of a spring (U = 0 at Δx = 0)
  • Electrostatic: Infinite separation of charges (U = 0 at r = ∞)
• Changing the zero point shifts the entire potential energy curve up or down, but differences in potential energy remain the same.

• The change in potential energy (ΔU) is equal to the negative work done by conservative forces:
  • $$\Delta U = - \int_{a}^{b} \vec{F}_{cf}(r) \cdot d\vec{r}$$
• Positive work by a conservative force decreases potential energy (think of a ball falling down).
• Negative work by a conservative force increases potential energy (think of lifting a ball).

#Analyzing Potential Energy Graphs

Potential energy graphs are like roadmaps of a system's behavior. Let's learn how to read them!

#Potential Energy Slope and Forces

• The conservative force in one dimension is the negative slope of the potential energy curve:
  • $$F_{x} = -\frac{dU(x)}{dx}$$
• Forces always point in the direction of decreasing potential energy.
• Steeper slopes mean larger forces, while flat regions mean zero force.

• Stable Equilibrium: Local minima (valleys) on the potential energy curve. If you nudge the system, it returns to this point (think of a ball at the bottom of a bowl). Concave up.
• Unstable Equilibrium: Local maxima (peaks) on the potential energy curve. If you nudge the system, it moves away (think of a ball balanced on top of a hill). Concave down.
• Neutral Equilibrium: Flat regions where the force is zero. If you nudge the system, it stays at the new position.

#Visualizing Equilibrium

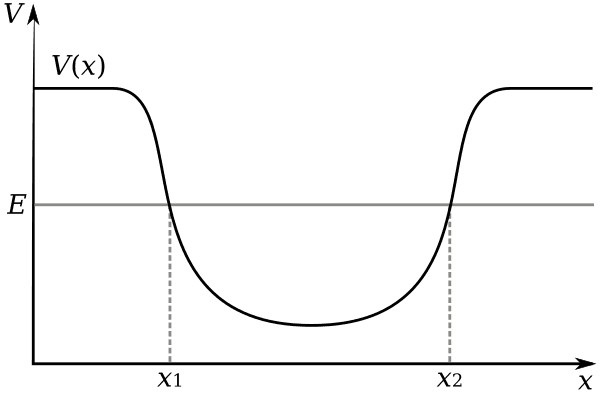
Potential energy graph showing stable and unstable equilibrium points.

#Common Potential Energy Systems

Let's look at the potential energy formulas for some common systems:

#Elastic Spring Potential Energy

• $$U_{s} = \frac{1}{2} k(\Delta x)^{2}$$
  • Where k is the spring constant and Δx is the displacement from equilibrium.
  • This is always positive, as it depends on the square of the displacement.

• Point Masses: $$U_{g} = -G \frac{m_{1}m_{2}}{r}$$
  • Where G is the gravitational constant, m1 and m2 are the masses, and r is their separation.
  • Note the negative sign, indicating that gravity is an attractive force.
• Near Earth's Surface: $$\Delta U_{g} = mg\Delta y$$
  • Where m is the mass, g is the acceleration due to gravity, and Δy is the change in height.

#Multiple-Object Systems

• The total potential energy is the sum of the potential energies of all pairs of interacting objects.
• For example, in a system with three objects (1, 2, and 3), the total potential energy is: U_total = U_12 + U_13 + U_23

• Conservative Forces: Remember GSE (Gravity, Spring, Electrostatic) as your go-to conservative forces.
• Potential Energy Slope: Think "downhill" for the direction of the force. Forces always try to move objects to lower potential energy.
• Equilibrium: Visualize a ball on a hill (unstable) or in a valley (stable) to remember the difference.

#Final Exam Focus

Okay, you're in the home stretch! Here's what to focus on for the exam:

• High-Value Topics: Potential energy calculations, interpreting potential energy graphs, and understanding the relationship between potential energy and conservative forces.
• Question Types: Expect a mix of multiple-choice questions (MCQs) testing definitions and calculations, and free-response questions (FRQs) requiring you to analyze potential energy graphs and apply formulas to complex systems.
• Time Management: Don't spend too much time on one problem. If you're stuck, move on and come back later.
• Common Pitfalls: Watch out for sign errors in potential energy calculations, especially with gravity. Always define your zero point for potential energy clearly.

• Review: Quickly go through the formulas and definitions one last time.
• Stay Calm: Take deep breaths and remember you've got this! You've prepared well, and now it's time to show what you know.
• Read Carefully: Pay close attention to the wording of each question. Don't make assumptions.

Practice Question

#Practice Questions

#Multiple Choice Questions

1. A particle moves along the x-axis under the influence of a conservative force. The potential energy of the particle is given by U(x) = 2x³ - 6x, where U is in joules and x is in meters. At what position x is the force on the particle equal to zero? (A) x = -1 m (B) x = 0 m (C) x = 1 m (D) x = 2 m

2. A spring with spring constant k is compressed by a distance x. If the spring is then compressed by a distance 2x, what is the ratio of the potential energy stored in the spring in the second case to the potential energy stored in the spring in the first case? (A) 1:1 (B) 1:2 (C) 2:1 (D) 4:1

#Free Response Question

A block of mass m is released from rest at the top of a frictionless ramp of height h. At the bottom of the ramp, it encounters a horizontal surface with a coefficient of kinetic friction μ. The block slides a distance d before coming to rest.

(a) Calculate the potential energy of the block at the top of the ramp. (b) Calculate the kinetic energy of the block at the bottom of the ramp. (c) Calculate the work done by friction as the block slides along the horizontal surface. (d) Calculate the distance d the block slides before coming to rest.

Scoring Guide

(a) 1 point - Correct potential energy formula: U = mgh

(b) 2 points - Recognizing conservation of energy: KE = PE - Correct kinetic energy value: KE = mgh

(c) 2 points - Correct work formula: W = -f_k * d - Correct friction force: f_k = μmg - Work done by friction: W = -μmgd

(d) 2 points - Setting work equal to change in KE: -μmgd = -mgh - Solving for d: d = h/μ