Introducing Statistics: Why Is My Sample Not Like Yours?
Jackson Hernandez
8 min read
Study Guide Overview
This AP Statistics study guide covers sampling distributions, including the Central Limit Theorem and standard error. It differentiates between discrete and continuous random variables and their calculations. The guide emphasizes distinguishing between population parameters and sample statistics, providing practice problems and focusing on exam strategies for multiple-choice and free-response questions.
#AP Statistics: Sampling Distributions & Parameters - Your Ultimate Review 🚀
Hey there, future AP Stats master! Let's get you prepped and confident for the exam. This guide is designed to be your go-to resource, especially the night before the test. We'll break down everything you need to know about sampling distributions, parameters, and statistics, making sure it all clicks into place. Let's dive in!
#Sampling Distributions: The Big Picture 🖼️
A sampling distribution is a distribution of a statistic (like a mean or proportion) calculated from all possible samples of a given size from a population. It's like taking a bunch of snapshots of the population and seeing how the statistics vary.
Think of it this way: instead of just one sample, we're looking at the distribution of the results we'd get from many samples. This helps us understand how much our sample statistic might vary from the true population parameter.
#What's the Point?
Sampling distributions help us understand:
- Sampling Variability: How much sample statistics vary from sample to sample.
- Accuracy of Estimates: How well a sample statistic estimates a population parameter.
- Basis for Inference: The foundation for hypothesis testing and confidence intervals.
#Visualizing Sampling Distributions

- Caption: This image shows how multiple samples from a population create a sampling distribution. Each dot represents a sample mean, and the distribution shows how these means vary.
#Key Concepts
-
Central Limit Theorem (CLT): 💡 A big deal! It states that the sampling distribution of the sample mean approaches a normal distribution as the sample size increases, regardless of the original population's distribution. This is why we can often use normal calculations even if the population isn't normal.
-
Standard Error: The standard deviation of a sampling distribution. It measures the variability of the sample statistic.
#Differences in Sampling Distributions
When dealing with differences in sample means or proportions:
- Variances Add: Always! When finding the variance of the difference between two statistics, add their variances.
- Standard Deviations: To get the standard deviation, take the square root of the combined variance.
- Means Subtract: For means, you can simply subtract them. ➖
#Random Variables: Discrete vs. Continuous 🤔
Random variables are variables whose values are numerical outcomes of a random phenomenon.
#Discrete Random Variables
- Definition: Variables that can only take on a finite number of values or a countable number of values (usually whole numbers). Think of counting things!
- Examples: Number of students in a class, number of heads when flipping a coin, etc.
- Mean (Expected Value):
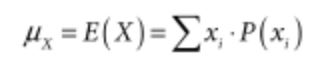
-
Standard Deviation:

#Continuous Random Variables
- Definition: Variables that can take on any value within a given range. Think of measuring things!
- Examples: Height, weight, temperature, time.
- Visualization: Use a histogram to display continuous data. 📊
#Parameters vs. Statistics: The Core Distinction 🎯
This is a crucial distinction! Always identify if you're dealing with a parameter or a statistic. It’s a frequent source of confusion, so nail this down!
#Population Parameters
- Definition: A measure that describes a characteristic of an entire population. It's a fixed, true value. 🌎
- Examples: Population mean (), population standard deviation (), population proportion ().
#Sample Statistics
- Definition: A measure that describes a characteristic of a sample. It's an estimate of the population parameter. 🏠
- Examples: Sample mean (), sample standard deviation (s), sample proportion ().
#The "P" and "S" Trick
Remember: Parameters describe Populations, and Statistics describe Samples.
Here's a handy table:
| Measurement | Population Parameter | Sample Statistic |
|---|---|---|
| Mean | 𝝁 | x̅ |
| Standard Deviation | σ | s |
| Proportions | 𝝆 | p̂ |
#Practice Problems: Test Your Knowledge 💪
Let's solidify your understanding with some practice. Remember to identify whether each scenario is describing a parameter or a statistic.
(1) A study finds that 750 out of 1000 sampled students have internet access at home. Is this a parameter or a statistic?
(2) The mean height of all adult males in the US is 70 inches. Is this a parameter or a statistic?
(3) A survey shows that 300 out of 500 sampled adults have a college degree. Is this a parameter or a statistic?
(4) The mean income of all US households is
(5) A study finds that 150 out of 200 sampled employees are satisfied with their job. Is this a parameter or a statistic?
#Answers
(1) Statistic. It's calculated from a sample.
(2) Parameter. It describes the entire population of adult males.
(3) Statistic. It's calculated from a sample.
(4) Parameter. It describes the entire population of US households.
(5) Statistic. It's calculated from a sample.
#Final Exam Focus 🎯
Okay, let's talk strategy for the big day! Here’s what to focus on:
#High-Priority Topics
- Sampling Distributions: Understand the concept, the Central Limit Theorem, and standard error.
- Parameters vs. Statistics: Be able to distinguish between them and know the symbols.
- Discrete vs. Continuous Random Variables: Know the difference and how to calculate means and standard deviations.
#Common Question Types
- MCQs: Expect questions that test your understanding of sampling variability and the CLT.
- FRQs: Be ready to explain the difference between parameters and statistics in context, and to calculate and interpret sampling distributions.
#Last-Minute Tips
- Time Management: Don’t get bogged down on one question. Move on and come back if you have time.
- Read Carefully: Pay close attention to wording in the questions.
- Show Your Work: Even if you make a mistake, you can still get partial credit for your method.
- Context is Key: Always interpret your results in the context of the problem.
#Practice Questions
<practice_question>
#Multiple Choice Questions
(1) A polling organization surveys 1000 randomly selected registered voters and asks if they support a particular candidate. The proportion of surveyed voters who support the candidate is a:
(A) parameter (B) statistic (C) population (D) sample (E) sampling distribution
(2) The standard deviation of the sampling distribution of the sample mean is called the:
(A) population standard deviation (B) sample standard deviation (C) standard error (D) margin of error (E) confidence interval
(3) Which of the following is NOT a characteristic of the sampling distribution of the sample mean?
(A) It is always normal if the population is normal. (B) It is approximately normal if the sample size is large enough. (C) Its mean is equal to the population mean. (D) Its standard deviation is smaller than the population standard deviation. (E) It is used to make inferences about the population mean.
#Free Response Question
A large university wants to estimate the average amount of money students spend on textbooks each semester. They take a random sample of 250 students and find that the sample mean is350 with a sample standard deviation of
(b) What is the sample statistic calculated in this study?
(c) Explain the concept of the sampling distribution of the sample mean in this context. What does it represent?
(d) Assuming the conditions for the Central Limit Theorem are met, describe the shape, center, and spread of the sampling distribution of the sample mean.
(e) If the university increased the sample size to 1000 students, how would this affect the sampling distribution of the sample mean? Explain.
#FRQ Scoring Guide
(a) The population parameter of interest is the average amount of money all students at the university spend on textbooks each semester. (1 point)
(b) The sample statistic calculated in this study is the sample mean of350. (1 point)
(c) The sampling distribution of the sample mean is the distribution of all possible sample means from samples of size 250 taken from the population of all students at the university. It represents the variability of the sample mean. (2 points)
(d) The shape of the sampling distribution is approximately normal due to the Central Limit Theorem. The center is the population mean (which is unknown but estimated by the sample mean of 100 / \sqrt{250} \approx 6.32$. (3 points)
(e) Increasing the sample size to 1000 would make the sampling distribution of the sample mean narrower (smaller standard error) and more closely approximate a normal distribution. The center would remain the same. (2 points)
You've got this! Go ace that exam! 🎉
Continue your learning journey

How are we doing?
Give us your feedback and let us know how we can improve





