AP Statistics: Chi-Square Goodness of Fit Test - The Ultimate Review

Hey, future AP Stats master! Let's nail this chi-square goodness of fit test. This guide is your fast track to acing the exam, focusing on what truly matters. Let's get started! 🚀

Chi-Square Goodness of Fit: Core Concepts

What is it?

The chi-square goodness of fit test is used to determine if an observed frequency distribution matches a theoretical expected distribution. Basically, are your observations what you'd expect, or is something fishy going on? 🤔

Big Picture Procedure

Here's the step-by-step breakdown:

1. Hypotheses:

   • Null Hypothesis (H₀): The observed distribution is the same as the expected distribution.
   • Alternative Hypothesis (Hₐ): The observed and expected distributions are significantly different.

2. Significance Level (α):

   • Choose your α (usually 0.1, 0.05, or 0.01). This is your threshold for rejecting H₀.

3. Chi-Square Statistic (χ²):

   • Calculate using the formula:

     $$\chi^2 = \sum \frac{(Observed - Expected)^2}{Expected}$$

     Where:

     • Observed = Observed frequency for each category

     • Expected = Expected frequency for each category

    ![Chi-Square Formula](https://zupay.blob.core.windows.net/resources/files/0baca4f69800419293b4c75aa2870acd_4f103d_2562.jpg?alt=media&token=55c8c403-f644-428f-b078-8e4b3a5af6a5)

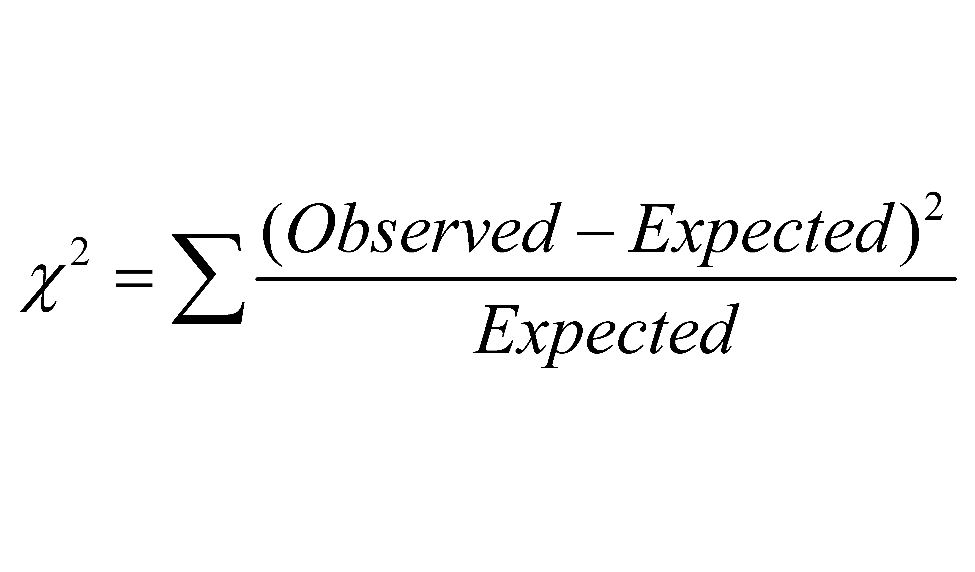
4. Degrees of Freedom (df): * df = Number of categories - 1

5. Critical Value:

   • Use a chi-square table or calculator to find the critical value based on your α and df.

6. Comparison:

   • If χ² statistic > critical value, reject H₀.
   • If χ² statistic ≤ critical value, fail to reject H₀.

7. Conclusion:

   • Reject H₀: Observed distribution is significantly different from expected.
   • Fail to reject H₀: Observed distribution is not significantly different from expected.

Doing the Test

Test Statistic (χ²)

• A χ² value close to 0 supports H₀ (observed and expected are similar).
• A large χ² value suggests that the expected counts are not accurate, leading to rejection of H₀.

Example: Happiness Survey

Let's say we have the following null hypothesis about happiness:

• 10% Unhappy (1)
• 15% Somewhat Unhappy (2)
• 28% Sometimes Happy/Sad (3)
• 30% Happy (4)
• 17% Always Happy (5)

We survey 1000 people and get:

• 120 respond 1
• 180 respond 2
• 220 respond 3
• 480 respond 4
• 0 respond 5

Steps:

1. Calculate expected counts: 100, 150, 280, 300, 170
2. Calculate (Observed - Expected)² / Expected for each category.
3. Sum these values to get χ².

Degrees of Freedom (df)

• df = Number of categories - 1
• In the happiness example, df = 5 - 1 = 4

P-Value

• The p-value is the probability of observing a χ² statistic as extreme as the one calculated, assuming H₀ is true. 🅿️
• A low p-value (less than α) leads to rejecting H₀.

Example: Happiness Survey (Continued)

After the calculation, we get the following output:

Conclusion

• Compare p-value to α.
• If p-value < α, reject H₀. There is convincing evidence for Hₐ.
• If p-value ≥ α, fail to reject H₀. There is not convincing evidence for Hₐ.
• Never say “accept” the null!
• Always include context in your conclusion.

Example: Happiness Survey Conclusion

Since our p-value (~0) < 0.05, we reject the null hypothesis. We have convincing evidence that at least one of the proportions for how people rank on the happiness scale is incorrect. 😔

Final Exam Focus

• High-Priority Topics: Chi-square goodness of fit test, hypothesis testing steps, p-value interpretation, degrees of freedom, and conclusion writing.
• Common Question Types:
  • Multiple-choice questions testing your understanding of the steps and concepts.
  • Free-response questions requiring you to perform a full chi-square test and interpret the results.
• Time Management: Practice using your calculator efficiently to save time on calculations. Focus on understanding the concepts rather than memorizing formulas.
• Common Pitfalls:
  • Forgetting to calculate expected counts correctly.
  • Mixing up observed and expected values.
  • Misinterpreting the p-value.
  • Not including context in the conclusion.

Practice Questions

Practice Question

Multiple Choice Questions

Question 1:

A researcher is testing if the distribution of colors in a bag of candies matches the company's stated proportions. The null hypothesis is that the observed distribution matches the expected distribution. After performing a chi-square goodness of fit test, the p-value is 0.03. Assuming a significance level of 0.05, what is the correct conclusion?

(A) Fail to reject the null hypothesis; there is not enough evidence to suggest the distribution of colors is different from the stated proportions. (B) Fail to reject the null hypothesis; there is enough evidence to suggest the distribution of colors is different from the stated proportions. (C) Reject the null hypothesis; there is not enough evidence to suggest the distribution of colors is different from the stated proportions. (D) Reject the null hypothesis; there is enough evidence to suggest the distribution of colors is different from the stated proportions.

Question 2:

In a chi-square goodness of fit test, what does the degrees of freedom represent?

(A) The number of observations in the sample. (B) The number of categories in the distribution. (C) The number of categories minus one. (D) The number of expected values.

Question 3:

Which of the following best describes the purpose of a chi-square goodness of fit test?

(A) To determine if there is a linear relationship between two quantitative variables. (B) To compare the means of two or more groups. (C) To determine if an observed frequency distribution matches a theoretical expected distribution. (D) To estimate a population proportion based on a sample.

Free Response Question

A researcher wants to investigate whether the distribution of car colors in a particular city matches the national distribution. The national distribution is as follows: 20% are white, 25% are black, 15% are silver, 10% are red, and 30% are other colors. The researcher observes 300 cars in the city and finds the following: 70 white, 80 black, 40 silver, 30 red, and 80 other.

(a) State the null and alternative hypotheses. (b) Calculate the expected frequencies for each color. (c) Calculate the chi-square test statistic. (d) Determine the degrees of freedom. (e) Using a significance level of 0.05, state your conclusion.

Scoring Breakdown:

(a) Hypotheses (1 point):

• H₀: The distribution of car colors in the city matches the national distribution.
• Hₐ: The distribution of car colors in the city does not match the national distribution.

(b) Expected Frequencies (1 point):

• White: 300 * 0.20 = 60
• Black: 300 * 0.25 = 75
• Silver: 300 * 0.15 = 45
• Red: 300 * 0.10 = 30
• Other: 300 * 0.30 = 90

(c) Chi-Square Statistic (2 points):

• χ² = [(70-60)²/60] + [(80-75)²/75] + [(40-45)²/45] + [(30-30)²/30] + [(80-90)²/90]
• χ² = 1.67 + 0.33 + 0.56 + 0 + 1.11 = 3.67

(d) Degrees of Freedom (1 point):

• df = 5 - 1 = 4

(e) Conclusion (2 points):

• Using a chi-square table or calculator, the critical value for α = 0.05 and df = 4 is approximately 9.488. * Since the calculated χ² (3.67) is less than the critical value (9.488), we fail to reject the null hypothesis.
• Conclusion: There is not enough evidence to suggest that the distribution of car colors in the city is different from the national distribution.

Alright, you've got this! Keep practicing, stay calm, and go ace that AP Stats exam! 🌟