
The IB Math Internal Assessment (IA) is your opportunity to dive deep into a mathematical topic that fascinates you. If you're taking Calculus, the world is your oyster when it comes to finding intriguing IA ideas. Here's a breakdown of a classic example and some other avenues to explore:
Optimizing a Cylindrical Can: A Classic Example
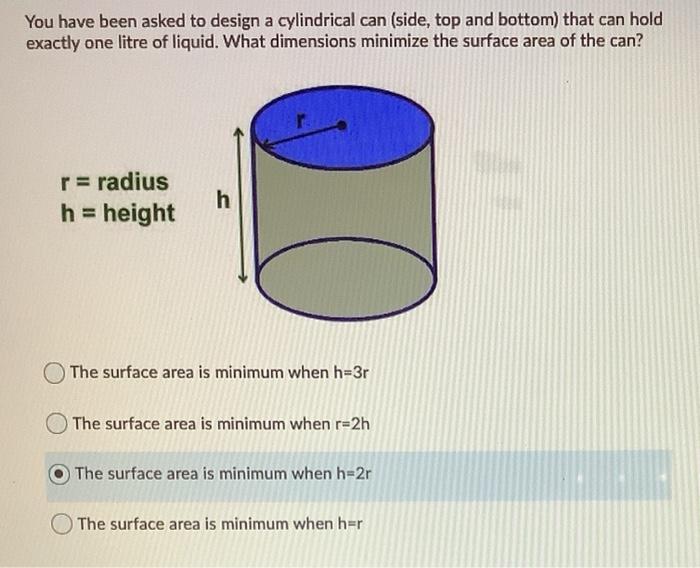
This IA idea revolves around a common question: How can we design a cylindrical can to hold a specific volume but use the least amount of material? This problem beautifully combines calculus concepts with real-world applications.
Here's how you can approach it:
- Define the Problem: Start by clearly stating the goal – to minimize the surface area (and thus, the material used) of a cylindrical can while keeping its volume constant.
- Formulate Equations: You'll need the formulas for the volume and surface area of a cylinder:
- Volume (V) = πr²h (where r is the radius and h is the height)
- Surface Area (SA) = 2πr² + 2πrh
- Single Variable Optimization: Use the constraint (fixed volume) to express one variable (like height) in terms of the other (radius). Substitute this into the surface area equation to get a function of a single variable (the radius).
- Calculus Time! This is where calculus shines. Find the derivative of the surface area function with respect to the radius. Set the derivative equal to zero and solve for the critical points (potential maximum or minimum values).
- Verify and Interpret: Use the second derivative test to confirm that you've found a minimum surface area. Discuss the relationship between the optimal radius and height. How do these dimensions affect the can's overall shape?
- Real-World Connection: Research standard can sizes for beverages or food products. Do they align with your calculated optimal dimensions? Why might there be differences?
More Exciting Calculus IA Ideas
The beauty of the IA is the freedom to explore. Here are some other calculus-based avenues:
1. Modeling Real-World Phenomena:
- Population Growth: Use differential equations to model and analyze population growth patterns of different species. Consider factors like carrying capacity and limiting resources.
- Spread of Diseases: Explore how mathematical models can predict the spread of infectious diseases. You can investigate the impact of vaccination rates or social distancing measures.
- Cooling/Heating Curves: Apply Newton's Law of Cooling (or Heating) to model the temperature change of an object over time. You could investigate factors influencing the cooling rate of a cup of coffee, for example.

2. Optimization Problems:
- Shortest Path: Use calculus to find the shortest path between two points on a curved surface (like a sphere). This has applications in navigation and mapmaking.
- Maximizing Area: Explore how to maximize the area of a shape with a fixed perimeter. You could investigate different polygons or even irregular shapes.
3. Related Rates Problems:
- Sliding Ladder: A classic problem involves a ladder sliding down a wall. Use related rates to find how fast the top of the ladder is moving as the bottom slides away from the wall.
- Expanding Balloon: Investigate how the radius of a balloon changes with respect to its volume as it is being inflated.
Key Tips for Success
- Choose a Topic You Love: Your enthusiasm will shine through in your writing.
- Keep It Focused: Don't try to do too much. A well-defined, in-depth exploration is better than a superficial overview of many topics.
- Show Your Work: Clearly explain your reasoning, calculations, and interpretations.
- Connect to the Real World: Discuss the implications and applications of your findings.
- Proofread Carefully: Ensure your IA is well-written and free of errors.
Remember, your Math IA is a journey of mathematical exploration. Embrace the challenge, and most importantly, have fun with it!