#Visualizing Asymptotes

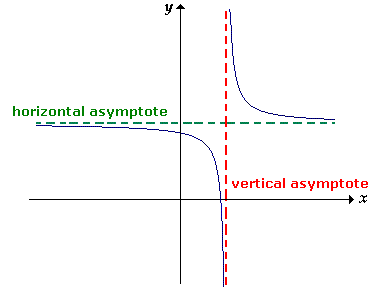
• Caption: The dashed vertical line is a vertical asymptote. The function gets closer and closer to this line, but never crosses it.

#Example: Putting It All Together

Let's look at the function:

$$r(x) = \frac{x + 1}{x^2 - 1}$$

1. Factor: Factor the denominator: r(x) = (x + 1) / ((x + 1)(x - 1)).
2. Identify Zeros: The denominator's zeros are x = -1 and x = 1.
3. Check Numerator: The numerator's zero is x = -1.
4. Simplify: Notice that we can simplify the function to r(x) = 1 / (x - 1), but remember that there is a hole at x=-1.
5. Vertical Asymptote: There's a vertical asymptote at x = 1 because the denominator is zero, and the numerator is not zero at that point.

#Limits and Asymptotes

• Behavior Near Asymptotes: As x approaches a vertical asymptote from the left or right, the function will approach either positive or negative infinity.

• One-Sided Limits:

  • $\lim_{x\to 1^-} \frac{x+1}{x^2-1} = -\infty$ (approaching from the left)
  • $\lim_{x\to 1^+} \frac{x+1}{x^2-1} = \infty$ (approaching from the right)

#

• Holes vs. Asymptotes: Don't confuse holes with vertical asymptotes. If a factor cancels out from both the numerator and denominator, you get a hole, not an asymptote, at that x-value.

#More Examples

• Caption: These examples show different rational functions and their vertical asymptotes. Practice identifying these in various functions.

#

• Factor First: Always factor the numerator and denominator to identify zeros and potential asymptotes.
• Check Multiplicities: Compare multiplicities to determine if you have an asymptote or a hole.
• Sketch It Out: Quickly sketch the graph to visualize the asymptotes and behavior of the function.

#Final Exam Focus

• High-Priority Topics:

  • Identifying vertical asymptotes from rational functions.
  • Determining the behavior of functions near asymptotes.
  • Distinguishing between holes and asymptotes.

• Common Question Types:

  • Multiple-choice questions asking for the vertical asymptotes of a given function.
  • Free-response questions requiring you to analyze the behavior of a function, including its asymptotes and limits.

• Last-Minute Tips:

  • Time Management: Don't spend too long on one question. Move on and come back if you have time.
  • Common Pitfalls: Watch out for sign errors and forgetting to check the multiplicity of zeros.
  • Strategies: If you're stuck, try sketching a quick graph or plugging in some test values to see the function's behavior.

#

Practice Question

Practice Questions

#Multiple Choice

1. What are the vertical asymptotes of the function $f(x) = \frac{x^2 - 4}{x^2 - 5x + 6}$? (A) x = 2, x = 3 (B) x = -2, x = -3 (C) x = 2 (D) x = 3

2. Which of the following functions has a vertical asymptote at x = -2? (A) $f(x) = \frac{x}{x-2}$ (B) $f(x) = \frac{x-2}{x+2}$ (C) $f(x) = \frac{x+2}{x-2}$ (D) $f(x) = \frac{x}{x^2+4}$

#Free Response

Consider the function $g(x) = \frac{x^2 - 9}{x^2 - 4x + 3}$.

(a) Identify all vertical asymptotes of the function. (b) Determine the limit of the function as x approaches each vertical asymptote from the left and right. (c) Does the function have any holes? If so, identify the x-coordinate of the hole.

Scoring Breakdown:

(a) Vertical Asymptotes (2 points): * 1 point for factoring the numerator and denominator correctly. * 1 point for identifying the correct vertical asymptotes.

(b) Limits (4 points): * 1 point for each limit from the left at each asymptote. * 1 point for each limit from the right at each asymptote.

(c) Holes (2 points): * 1 point for identifying the presence of a hole. * 1 point for stating the correct x-coordinate of the hole.

#Answers

Multiple Choice:

1. D
2. B

Free Response: (a) Vertical Asymptote: x = 1 (b) $\lim_{x\to 1^-} g(x) = \infty$, $\lim_{x\to 1^+} g(x) = -\infty$ (c) Yes, there is a hole at x = 3

Remember, you've got this! Keep practicing, and you'll ace that exam. Good luck! 🍀