Sampling Methods: Your Guide to Gathering Data Like a Pro 📊

Hey there, future AP Stats superstar! Let's dive into the world of sampling methods. Remember, the way we collect data shapes what we can say about a population. So, let's make sure we're doing it right!

Types of Non-Biased Sampling Methods

To avoid bias, we use random sampling methods. Here's a breakdown of the most common ones:

Simple Random Sample (SRS)

An SRS is like picking names out of a hat. Every individual, and every group of individuals, has an equal chance of being chosen. It's the gold standard for unbiased sampling. 🃏

• Key Idea: Each member of the population has an equal chance of being selected.

• How to: Number everyone, then use a random number generator (like on your TI-84) to select your sample.

• Calculator Steps: 1. Label each individual from 1 to N. 2. Use randInt(1, N, n) to generate n random integers. 3. Select the individuals corresponding to those numbers.

• Sampling without replacement: Once an individual is chosen, they can't be chosen again.
• Sampling with replacement: An individual can be chosen multiple times.

Stratified Random Sample

Imagine dividing your population into groups (strata) based on shared characteristics, then taking an SRS from each group. That's a stratified random sample. 📚

• Key Idea: Divide the population into strata (groups) based on shared characteristics, then take an SRS from each stratum.
• Why use it? When you have a heterogeneous population, it ensures that your sample represents all subgroups.
• Example: If studying diet and heart disease, stratify by age, gender, and income to get a representative sample.

Caption: Stratified sampling ensures representation from all subgroups.

Cluster Sample

Divide the population into clusters (groups), randomly select a few clusters, and then sample everyone in those clusters. That's cluster sampling. 🏘️

• Key Idea: Divide the population into clusters, randomly select a few clusters, and then sample everyone in those clusters.
• Why use it? When it's too hard or expensive to sample individuals directly (e.g., studying attitudes in high schools across a city).
• Example: Randomly select a few high schools in a city, then survey all students in those schools.

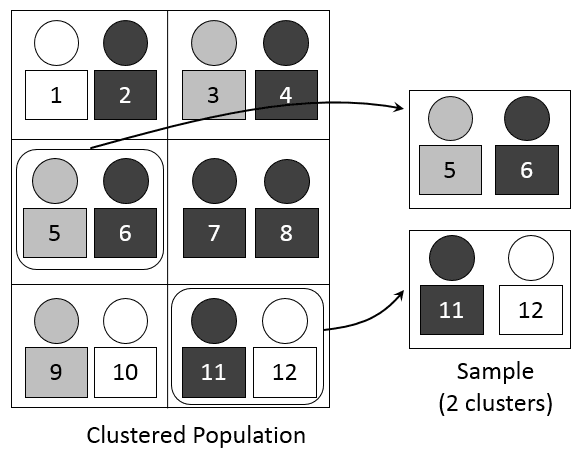
Caption: In cluster sampling, entire groups are chosen.

Systematic Random Sample

Choose a random starting point, then select every kth member of the population. That's a systematic random sample. 🚶

• Key Idea: Select a random starting point, then select every kth member.

• Why use it? It's easy to implement and can be more efficient than SRS.

• Example: If you want to survey 100 people from a list of 1000, pick a random starting point (say, the 5th person), then select every 10th person after that.

Caption: A visual guide to different sampling methods.

Practice Problem

Let's put this into practice. You want to study college students' attitudes towards climate change with a budget of $10,000 and six months. Which method is best?

• Simple Random Sampling: Create a list of all U.S. college students and use a random number generator. (Accurate, but time-consuming and expensive.)
• Cluster Sampling: Divide students into geographic clusters (e.g., East Coast, West Coast) and randomly select a few clusters. (Efficient, but clusters must be representative.)
• Systematic Random Sampling: Create a list of all students, choose a random starting point, then select every 100th student. (Easy to implement, but potential for bias if the interval is not random.)

Answer

In this situation, cluster sampling is often the most practical choice. It's more efficient and cost-effective than SRS, and you don't need a complete list of all students. However, you must ensure clusters are representative of the population to avoid bias.

Understanding the differences between these sampling methods is crucial for both multiple-choice and free-response questions. Pay special attention to the advantages and disadvantages of each method.

Alternative Answers

Here's the fun part: AP Stats graders are actually open-minded if you picked either simple random sampling or systematic random sampling (instead of cluster sampling). Your job is to create a very persuasive argument that'll convince them that either sampling method might work, too (in comparison to the other two)!

Final Exam Focus

• High-Priority Topics: - Distinguishing between different sampling methods (SRS, stratified, cluster, systematic). - Identifying potential biases in sampling. - Understanding the strengths and weaknesses of each method.
• Common Question Types: - Multiple-choice questions asking you to identify the type of sampling method used in a scenario. - Free-response questions asking you to design a sampling plan or critique a given method.
• Last-Minute Tips: - Time Management: Quickly identify the type of sampling method in questions. Don't overthink it! - Common Pitfalls: Avoid confusing stratified and cluster sampling. Always consider potential sources of bias. - Strategies: When designing a sampling plan, clearly explain your reasoning and justify your choices.

Practice Questions

Practice Question

Multiple Choice Questions

1. A researcher wants to study the opinions of college students on a new tuition policy. They randomly select 50 students from each of the four class levels (freshman, sophomore, junior, and senior). What type of sampling method is used? (a) Simple Random Sample (b) Stratified Random Sample (c) Cluster Sample (d) Systematic Random Sample

2. A school district wants to assess student satisfaction with their school's facilities. They randomly select 10 schools and survey all students in those schools. What type of sampling method is used? (a) Simple Random Sample (b) Stratified Random Sample (c) Cluster Sample (d) Systematic Random Sample

3. A company wants to survey its employees. They have a list of all employees and select every 20th employee to participate in the survey. What type of sampling method is used? (a) Simple Random Sample (b) Stratified Random Sample (c) Cluster Sample (d) Systematic Random Sample

Free Response Question

A large university wants to conduct a survey to determine student opinions on a proposed change to the academic calendar. The university has a diverse student body, including undergraduate and graduate students, students from different colleges (e.g., engineering, arts, business), and students living on and off campus.

(a) Describe how you would use a stratified random sampling method to select 200 students for the survey. Clearly explain each step of your process.

(b) Explain one advantage of using stratified random sampling over simple random sampling in this scenario.

(c) Describe a potential source of bias that could arise if the university used a cluster sampling method instead of stratified random sampling. How could this bias affect the results of the survey?

Scoring Guidelines

(a) (4 points) - (1 point) Identify relevant strata (e.g., undergraduate/graduate, college, on/off campus). - (1 point) Explain how to take an SRS from each stratum (e.g., number students and use a random number generator). - (1 point) Specify the number of students to be selected from each stratum to reach a total of 200. - (1 point) Clearly state how to combine the samples to form the final sample.

(b) (1 point) - Explain that stratified sampling ensures representation from all subgroups, reducing variability and potentially leading to more accurate results compared to simple random sampling.

(c) (2 points) - (1 point) Describe a potential source of bias (e.g., if clusters are based on dorms, students in certain dorms might have similar opinions). - (1 point) Explain how this bias could affect results (e.g., over- or underrepresentation of certain opinions).

You've got this! Keep reviewing, stay confident, and you'll ace that AP Stats exam. 🚀