#AP Chemistry: Gases - The Night Before 🚀

Hey there, future AP Chem master! Let's make sure you're feeling confident about gases. We'll break down everything you need to know, focusing on key concepts and test-taking strategies. Let's get started!

#Kinetic Molecular Theory (KMT) and Ideal Gases

First, let's recap the five assumptions of the Kinetic Molecular Theory (KMT) which describes the behavior of ideal gases:

1. No attractive or repulsive forces between gas particles.
2. Gas particles have negligible volume compared to the space between them.
3. Gas particles move in random, constant, straight-line motion.
4. Collisions are elastic (no energy loss).
5. Average kinetic energy of gas particles is directly proportional to temperature (KE = 1/2mv²). All gases have the same average KE at a given temperature.

# When Do Gases Deviate from Ideal Behavior? 🤨

Real gases deviate from ideal behavior under conditions of low temperatures and high pressures. Here's why:

#➡️⬅️ Attractive Forces Become Significant

• At low temperatures 🌡️, gas particles slow down and spend more time near each other, increasing attractive forces.
• Polar molecules and larger molecules have stronger intermolecular forces (IMFs), causing them to deviate more from ideal behavior.

#Significant Particle Volume

• At high pressure, the volume of the container decreases, making the volume of the gas particles more significant.

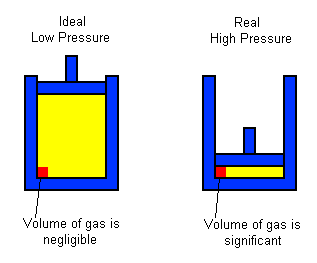
• Image Caption: As pressure increases, the volume of the gas decreases, and the volume of the gas particles becomes a more significant proportion of the total volume.

#Graphically Speaking

• The graph below shows that as pressure increases, the value of PV/RT deviates from 1 (the ideal value).

• Image Caption: Deviation from ideal gas behavior increases with pressure. Ideal gases should have a PV/RT value of 1. ### Correcting the Ideal Gas Law: The Van der Waals Equation 🤓

Chemists use the Van der Waals equation to correct for non-ideal behavior:

• The equation corrects pressure (P) and volume (V) to account for IMFs and particle volume.
• +a corrects the pressure because real gas pressure is lower.
• -b corrects the volume because real gas volume is higher.

# Diffusion and Effusion 💨

#Diffusion

• Diffusion is the mixing of gases.
• Temperature ⬆️, rate of diffusion ⬆️ (faster particles).
• Molecular size ⬆️, rate of diffusion ⬇️ (slower, heavier particles).

• Image Caption: Lighter gases diffuse faster than heavier gases.

#Effusion

• Effusion is the passage of gas through a tiny hole into a vacuum.
• Same rules as diffusion: Temperature ⬆️, rate of effusion ⬆️; Molecular size ⬆️, rate of effusion ⬇️.

• Image Caption: Effusion is the escape of gas through a small hole.

# Graham's Law of Effusion

• Graham's Law relates the rate of effusion to the molar mass of the gas:

Where: * Rate1 is the rate of effusion of gas 1 * Rate2 is the rate of effusion of gas 2 * M2 is the molar mass of gas 2 * M1 is the molar mass of gas 1

# Final Exam Focus 🎯

• High-Priority Topics:
  • Conditions for deviations from ideal gas behavior (low T, high P).
  • Effect of IMFs on real gas pressure and volume.
  • Graham's Law and its applications.
• Common Question Types:
  • MCQs testing conceptual understanding of KMT and deviations.
  • FRQs requiring explanations of non-ideal behavior.
  • Problems involving Graham's Law.
• Last-Minute Tips:
  • Read questions carefully, especially FRQs. Identify what is being asked.
  • Show all your work for FRQs, even if it seems simple.
  • Don't leave any question blank. Partial credit is your friend.
  • Manage your time wisely. Don't spend too long on a single question.
  • Stay calm and believe in yourself! You've got this!

# Practice Questions

Practice Question

Multiple Choice Questions

1. Under which of the following conditions does a real gas behave most like an ideal gas? (A) High temperature and high pressure (B) High temperature and low pressure (C) Low temperature and high pressure (D) Low temperature and low pressure

2. Which of the following gases would have the highest rate of effusion at the same temperature? (A) O2 (B) N2 (C) CO2 (D) He

Free Response Question

Consider two gases, nitrogen (N2) and oxygen (O2), in separate containers at the same temperature.

(a) Compare the average kinetic energy of the gas molecules in the two containers. Explain your reasoning.

(b) Compare the average speed of the gas molecules in the two containers. Explain your reasoning.

(c) If both gases are allowed to effuse through a small opening, which gas will effuse faster? Calculate the ratio of their effusion rates.

(d) Under what conditions would the behavior of these gases deviate significantly from the ideal gas law? Explain why these conditions cause deviations.

Scoring Breakdown

(a) (1 point) The average kinetic energy is the same since both gases are at the same temperature. Kinetic energy is directly proportional to temperature.

(b) (1 point) The average speed of N2 molecules is greater than O2 molecules. Because KE = 1/2mv^2, and KE is the same, the lighter molecule (N2) must have a higher velocity.

(c) (2 points) N2 will effuse faster. Rate of effusion of N2 / Rate of effusion of O2 = sqrt(32/28) = 1.07. N2 effuses 1.07 times faster than O2. (d) (2 points) Gases deviate from ideal behavior at low temperatures and high pressures. At low temperatures, the gas molecules move slower, and attractive forces become more significant. At high pressure, the volume of the gas molecules becomes significant compared to the container volume.

Remember, you've got this! Go ace that exam! 💪