Kinematics Overview and Motion in One Dimension
John Smith
10 min read
Listen to this study note
Study Guide Overview
This AP Physics C: Mechanics study guide covers kinematics, focusing on motion in one dimension. Key concepts include position, displacement, distance, velocity, speed, and acceleration. It differentiates between scalars and vectors, explores average vs. instantaneous velocity, and details the kinematic equations. Calculus applications, specifically derivatives and integrals, relating position, velocity, and acceleration are explained. Finally, the guide covers interpreting kinematic graphs and provides practice questions and exam tips.
#AP Physics C: Mechanics - Unit 1: Kinematics Study Guide 🚀
Hey there, future physicist! Let's get you prepped and confident for your AP Physics C: Mechanics exam. This guide is designed to be your go-to resource, especially the night before the test. Let's dive in!
#1. Introduction to Kinematics
Kinematics is all about describing motion—how things move, without worrying about why they move. It's a foundational unit, so mastering these concepts is crucial. Think of it as the ABCs of motion! 🚗💨
#Big Ideas 💡
- Change: Interactions cause changes in motion. This means forces are involved, but in kinematics, we focus on describing how the motion changes, not the forces causing it.
- Example: Why do you speed up as you roll down a hill? Kinematics describes how your speed increases, while dynamics (later units) will explain why (forces like gravity).
- Projectile Motion: Throwing a stone higher can increase the distance it travels. Kinematics helps us understand the trajectory and range.
#Exam Impact
- Weight: 14-20% of the exam. This is a significant portion, so make sure you're solid on these concepts!
- Time: Approximately 22 class periods (45 min each).
- Practice: Use the AP Classroom progress checks (15 MCQs, 1 FRQ) to gauge your understanding.
#2. Kinematics: Motion in One Dimension
Let's break down the key terms you'll need to describe motion along a straight line:
#Key Terms 📝
- Position: An object's location at a specific time.
- Displacement (Δx): Change in position relative to some origin.
- Distance: Total path length covered by the object.
Distance is always positive, while displacement can be negative!
- Velocity: Rate of change of displacement over time.
Velocity is a vector!
- Speed: Rate of change of distance over time.
Speed is always positive, while velocity can be negative!
- Acceleration: Rate of change of velocity over time.
Acceleration is a vector!
#Scalars vs. Vectors 🧭
- Vector Quantities: Displacement, velocity, and acceleration have both magnitude (numerical value) and direction. Think of them as arrows pointing in a specific way.
- Scalar Quantities: Distance and speed have only magnitude (no direction). They're just numbers.
#Visualizing the Difference
Look at the image below. The bicyclist's distance is the length of path A, while the displacement is the straight-line path B.

Image from Dan Levine
- Positive (+): Up or right direction.
- Negative (-): Down or left direction.
#Visualizing Vectors
Here's another visual to help you see how displacement, velocity, and acceleration are related as vectors:

Image from Online Math Learning
#Average vs. Instantaneous Velocity ⏱️
-
Average Velocity: Displacement divided by the total time interval. It's an approximation of motion, as the velocity might have changed during that time.

-
Instantaneous Velocity: Velocity at a specific moment in time. You can find this by taking the derivative of the position function.
Derivatives give you the rate of change at a specific point, while integrals give you the total change over an interval.
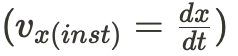
#Kinematic Equations
Here are the key equations that describe the relationships between position (x), velocity (v), acceleration (a), and time (t).
Remember these equations—they're your best friends! You can use the acronym SUVAT to remember the variables involved: S (displacement), U (initial velocity), V (final velocity), A (acceleration), T (time).


Tip: Practice solving for any variable in these equations, given the others. This will help you in problem-solving!
And one more useful equation:

#Calculus in Kinematics 🧮
- Derivatives: The derivative of the position function gives you the velocity function, and the derivative of the velocity function gives you the acceleration function. ,
- Integrals: The integral of the acceleration function gives you the velocity function, and the integral of the velocity function gives you the position function. ,
Here's a quick refresher on basic derivatives and integrals:

#Tips for Using Calculus
- Definitions: Understand that displacement, velocity, and acceleration are related through derivatives and integrals.
- Derivatives: Use derivatives to find velocity from position and acceleration from velocity.
- Formulas: Remember the basic kinematic equations, but also know how to derive them using calculus.
- Units: Always use the correct units (m, m/s, m/s²).
- Reference Frame: Consider your reference frame when solving problems.
- Graphs: Use graphs to visualize motion. The slope of a position-time graph is velocity, and the slope of a velocity-time graph is acceleration.
- Practice: The more you practice, the better you'll get!
#Kinematic Graphs 📈
Here's how to interpret kinematic graphs:
| Types of Kinematic Graphs | Area Under Curve | Slope | Magnitude of Y-value |
|---|---|---|---|
| Position vs. Time | N/A | Velocity | Distance from detector or starting position |
| Velocity vs. Time | Change in Position | Acceleration | Speed of Object |
| Acceleration vs. Time | Change in Velocity | Jerk* (Not Tested in AP Exam) | Acceleration |
#Vector Quantity Table 📊
Here's a table to help you understand the meaning of positive, negative and zero values for vector quantities:
| Vectorxa0 | Negative (-) | Zero (0) | Positive (+) |
|---|---|---|---|
| Displacement | You are now south, west, left, or in the -x or -y direction of your starting position. | You are back at your starting position. | You are now north, east, right, or in the +x or +y direction of your starting position. |
| Velocity | You are traveling south, west, left, or in the -x or -y direction. | You are at rest. | You are traveling north, east, right, or in the +x or +y direction. |
| Acceleration | If your velocity > 0, your speed is decreasing in a positive direction. If your velocity < 0, your speed is increasing in a negative direction. | You are at restxa0ORxa0you are moving at a constant velocity. | If your velocity > 0, your speed is increasing in a positive direction. If your velocity < 0, your speed is decreasing in a negative direction. |
#Final Exam Focus
Okay, let's focus on what's most important for the exam:
- High-Priority Topics:
- Kinematic equations and their applications.
- Understanding the difference between average and instantaneous velocity.
- Using calculus (derivatives and integrals) in kinematics.
- Interpreting kinematic graphs (position-time, velocity-time, acceleration-time).
- Vector vs. scalar quantities.
- Common Question Types:
- Multiple-choice questions testing conceptual understanding of displacement, velocity, and acceleration.
- Free-response questions involving kinematic equations, calculus, and graphical analysis.
- Time Management:
- Quickly identify the type of problem and the required concepts.
- Don't spend too much time on one question. Move on and come back if time permits.
- Common Pitfalls:
- Mixing up distance and displacement, speed and velocity.
- Forgetting to consider the direction of vector quantities.
- Incorrectly applying calculus rules.
- Misinterpreting kinematic graphs.
- Strategies:
- Draw diagrams to visualize the problem.
- Write down all knowns and unknowns.
- Choose the appropriate equations.
- Check your units and answers.
#Practice Questions
Let's test your knowledge with some practice questions:
Practice Question
#Multiple Choice Questions
-
A car accelerates uniformly from rest to a speed of 20 m/s in 5 seconds. What is the average acceleration of the car? (A) 2 m/s² (B) 4 m/s² (C) 5 m/s² (D) 10 m/s²
-
A ball is thrown vertically upward. Which of the following is true about the ball's velocity and acceleration at its highest point? (A) Both velocity and acceleration are zero. (B) Velocity is zero, but acceleration is nonzero. (C) Velocity is nonzero, but acceleration is zero. (D) Both velocity and acceleration are nonzero.
-
A particle moves along the x-axis with its position given by x(t) = 2t³ - 6t² + 5t. What is the acceleration of the particle at t = 2 seconds? (A) 0 m/s² (B) 6 m/s² (C) 12 m/s² (D) 24 m/s²
#Free Response Question
A 2 kg block is released from rest at the top of a frictionless ramp inclined at 30° to the horizontal. The ramp is 5 meters long.
(a) Draw a free-body diagram of the block on the ramp. (2 points) (b) Determine the acceleration of the block down the ramp. (3 points) (c) Determine the speed of the block at the bottom of the ramp. (3 points) (d) If the ramp were rough with a coefficient of kinetic friction of 0.2, how would the acceleration of the block be affected? Explain qualitatively. (2 points)
#FRQ Scoring Rubric
(a) Free-Body Diagram (2 points)
- 1 point for correctly drawing the gravitational force (weight) vector pointing downwards.
- 1 point for correctly drawing the normal force vector perpendicular to the ramp.
(b) Acceleration (3 points)
- 1 point for resolving the gravitational force into components parallel and perpendicular to the ramp.
- 1 point for correctly applying Newton's second law along the ramp:
- 1 point for the correct value of acceleration:
(c) Speed at the Bottom (3 points)
- 1 point for using a kinematic equation to relate final velocity, initial velocity, acceleration, and displacement:
- 1 point for correctly plugging in the values:
- 1 point for the correct final speed:
(d) Effect of Friction (2 points)
- 1 point for stating that friction would reduce the acceleration.
- 1 point for explaining that friction acts in the opposite direction of motion, reducing the net force and thus the acceleration.
Practice Question
#Answer to the Practice Question in the notes
The correct answer is D. To show a constant acceleration on a velocity vs. time graph, you need to consider the slope of each line segment. For constant acceleration, it is shown through a straight slope (not curved) on a velocity vs. time graph; therefore, QR cannot be it. For acceleration to be nonzero as well, the slope of the velocity vs. time graph cannot be horizontal, marking out PQ and TU. Therefore, RS & ST satisfy the question.
Continue your learning journey

How are we doing?
Give us your feedback and let us know how we can improve





