#AP Physics C: Mechanics - 2D Kinematics Study Guide 🚀

Hey there, future physicist! Ready to tackle motion in two dimensions? This guide will help you master projectile motion and 2D kinematics, so you can confidently ace your AP exam. Let's dive in!

#2D Kinematics: Projectile Motion

#What is Projectile Motion?

Projectile motion describes the path of an object launched into the air, influenced only by gravity (we're neglecting air resistance here, as the AP exam usually does!). Think of a thrown baseball, a kicked soccer ball, or even a launched rocket (before it starts using its engines).

• Trajectory: The curved path a projectile follows.
• Parametric Equations: We use equations that describe the projectile's position (x, y) at any given time (t): x(t) and y(t).
• Initial Velocity (v₀): The launch velocity sets the stage for the trajectory's shape.
• Gravity's Role: Acceleration due to gravity (g ≈ 9.8 m/s² or 10 m/s² for quick estimates) is constant and acts downwards (-g), affecting the vertical velocity (v_y).
• Calculus Connection: Derivatives of position equations give us velocity and acceleration. We can also use calculus to find max height and range.

*Image from DKPhysics*

#Key Concepts 💡

• Horizontal Velocity (v_x): Stays constant throughout the motion (no horizontal acceleration, if we ignore air resistance).
• Vertical Velocity (v_y): Changes due to gravity. It decreases as the object goes up and increases as it falls down.
• Independence of Motion: Horizontal and vertical motions are independent, but they are linked by time. The time it takes to go up is the same time it takes to come down (if you start and end at the same height).
• Max Height: At the peak of the trajectory, v_y = 0. This is a crucial point for solving many problems.

#Velocity Components

Let's break down the velocity into its x and y components:

• X-Direction:

  
  • v_x = v₀ * cos(θ) (Initial horizontal velocity)
  • x = v_x * t (Horizontal position at time t)
  • a_x = 0 (No horizontal acceleration)

• Y-Direction:

  
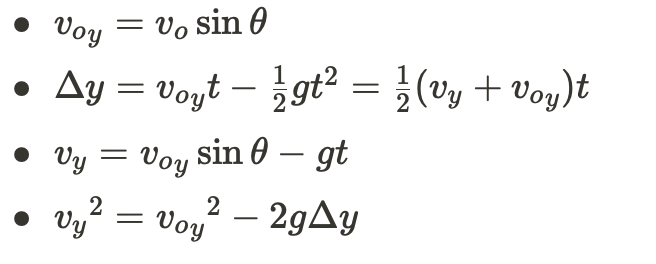  • v_y = v₀ * sin(θ) - gt (Vertical velocity at time t)
  • y = v₀ * sin(θ) * t - 1/2 * gt² (Vertical position at time t)
  • a_y = -g (Vertical acceleration due to gravity)


#Formula Sheet & Kinematic Equations

Don't panic about memorizing all those equations! The AP formula sheet is your friend. The first three equations on the sheet are the most useful for this unit. They can be adapted for both x and y directions.

*Image from collegeboard.org*
*Image from QS Study*

#Example: Finding Time to Max Height

Let's use the equation v_y = v_y₀ + a_y * t to find the time it takes to reach the max height. At max height, v_y = 0, a_y = -g, and v_y₀ = v₀ * sin(θ).


Substituting the values:


So, t = (v₀ * sin(θ)) / g. This is a handy formula to remember!

#Interactive Simulation

Want to see projectile motion in action? Check out this PhET Simulation to play around with different factors.

#Calculus in 2D Kinematics

• Position-Time Graphs: Visualize the motion. The slope gives you velocity.
• Velocity-Time Graphs: The slope here is acceleration.
• Equations of Motion: Use equations like x(t) = x₀ + v₀t + 1/2at² to find position, velocity, or acceleration given initial conditions.
• Displacement: The change in position. Average velocity is total displacement over time.
• Integration: Use integration to find displacement and average velocity from a velocity function.
• Fundamental Theorem of Calculus: Connects velocity and position functions.
• Direction: Always consider the direction of motion. A negative sign is important!

#Kinematics Practice Questions

Let's test your knowledge with some practice questions!

Practice Question

Question 1:

*Image from New Jersey Center for Teaching & Learning*

Answer:

The correct answer is C. We only care about the vertical motion here. Use the equation:


Since the initial vertical velocity (v_oy) is 0, the equation simplifies to:


Solving for t, you get approximately 0.7 seconds.

Practice Question

Question 2:

*Image from collegeboard.org*

Answer:

The correct answer is C. The only acceleration is the downward acceleration of gravity (-9.8 m/s²).

• A is wrong: Vertical velocity is 0 at point P.
• B is wrong: Horizontal velocity is constant.
• D is wrong: Speed is not constant, especially at point P.
• E is wrong: Displacement depends on the starting point.

Practice Question

Question 3:

*Image from New Jersey Center for Teaching & Learning*

Answer:

The correct answer is A. Use trigonometry to find the components:


Then calculate:


Exam Tip

Double-check if the problem requires degrees or radians!

Practice Question

Question 4:


Answer:

The correct answer is E. Acceleration is the derivative of velocity. The derivative rule for e^u is:


Applying this, you get E.

#Final Exam Focus 🎯

#High-Priority Topics:

• Projectile Motion: Understand the independence of horizontal and vertical motion. Know how to use kinematic equations to solve for time, distance, and velocity.
• Calculus Applications: Be comfortable using derivatives and integrals to analyze motion.
• Problem-Solving: Practice breaking down complex problems into simpler steps. Always start with what you know and what you need to find.

#Common Question Types:

• Finding max height, range, and time of flight.
• Analyzing motion with given initial conditions.
• Using calculus to find velocity and acceleration.
• Combining 2D kinematics with other concepts (like energy or momentum).

#Last-Minute Tips:

• Time Management: Don't spend too long on one question. If you're stuck, move on and come back later.
• Common Pitfalls: Be careful with signs (especially with gravity). Watch out for unit conversions.
• Strategies: Draw diagrams to visualize problems. Break down vectors into components. Use the formula sheet wisely.